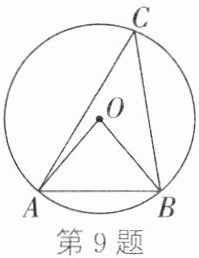
9. 如图,$\triangle ABC$是$\odot O$的内接三角形,$∠C=40^{\circ}$,连接$OA$、$OB$,则$∠OAB=$$^{\circ}$.

答案:
$50$
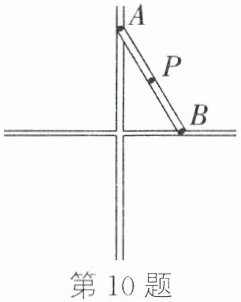
10. 著名画家达·芬奇曾经设计过一种如图所示的圆规,有两个互相垂直的滑槽(滑槽的宽度忽略不计),一根没有弹性的木棒两端$A$、$B$能在滑槽内自由滑动,将笔插入位于木棒中点$P$处的小孔中,随着木棒的滑动就可以画出一个圆. 若$AB=20cm$,则画出的圆的半径为$cm$.

答案:
10
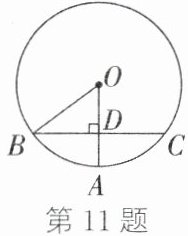
11. 如图,$OA$是$\odot O$的半径,弦$BC⊥OA$于点$D$,连接$OB$. 若$\odot O$的半径为5cm,$BC$的长为8cm,则$OD$的长是$cm$.

答案:
3
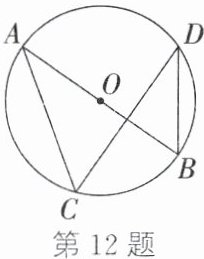
12. 如图,$\odot O$的直径$AB$平分弦$CD$(不是直径). 若$∠D=35^{\circ}$,则$∠C=$$^{\circ}$.

答案:
1. 首先,根据垂径定理:
因为$\odot O$的直径$AB$平分弦$CD$(不是直径),所以$AB\perp CD$,设垂足为$E$,则$\angle AEC = \angle AED=90^{\circ}$。
2. 然后,在$\triangle ADE$中:
已知$\angle D = 35^{\circ}$,$\angle AED = 90^{\circ}$,根据三角形内角和定理$\angle A+\angle D+\angle AED = 180^{\circ}$,可得$\angle A=180^{\circ}-\angle D - \angle AED$。
把$\angle D = 35^{\circ}$,$\angle AED = 90^{\circ}$代入,得$\angle A=180^{\circ}-90^{\circ}-35^{\circ}=55^{\circ}$。
3. 最后,根据同弧所对的圆周角相等:
因为$\angle C$与$\angle A$都是$\overset{\frown}{BD}$所对的圆周角,根据圆周角定理:同弧或等弧所对的圆周角相等,所以$\angle C=\angle A$。
所以$\angle C = 55^{\circ}$。
故答案为:$55$。
因为$\odot O$的直径$AB$平分弦$CD$(不是直径),所以$AB\perp CD$,设垂足为$E$,则$\angle AEC = \angle AED=90^{\circ}$。
2. 然后,在$\triangle ADE$中:
已知$\angle D = 35^{\circ}$,$\angle AED = 90^{\circ}$,根据三角形内角和定理$\angle A+\angle D+\angle AED = 180^{\circ}$,可得$\angle A=180^{\circ}-\angle D - \angle AED$。
把$\angle D = 35^{\circ}$,$\angle AED = 90^{\circ}$代入,得$\angle A=180^{\circ}-90^{\circ}-35^{\circ}=55^{\circ}$。
3. 最后,根据同弧所对的圆周角相等:
因为$\angle C$与$\angle A$都是$\overset{\frown}{BD}$所对的圆周角,根据圆周角定理:同弧或等弧所对的圆周角相等,所以$\angle C=\angle A$。
所以$\angle C = 55^{\circ}$。
故答案为:$55$。
13. 用一个圆心角为$126^{\circ}$,半径为10cm的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为$cm$.
答案:
3.5
14. 如图,在矩形$ABCD$中,分别以点$A$和$C$为圆心,$AD$为半径画弧,两弧有且仅有一个公共点. 若$AD=4$,则图中涂色部分的面积为.
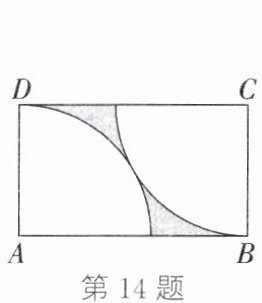

答案:
$16\sqrt{3}-\frac{16\pi}{3}$
15. 如图,在$\triangle AOB$中,$∠AOB=90^{\circ}$,$OA=OB=4\sqrt{2}$,$\odot O$的半径为2,$P$是边$AB$上的动点,过点$P$作$\odot O$的一条切线$PQ$($Q$为切点),则$PQ$长的最小值为.
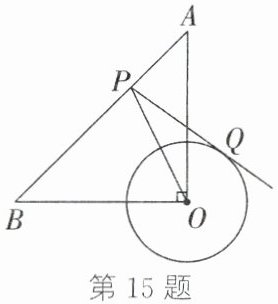

答案:
2√3
16. 如图,在平面直角坐标系中,点$A$、$B$、$P$的坐标分别为$(1,0)$、$(2,5)$、$(4,2)$. 若点$C$在第一象限内,且横、纵坐标均为整数,点$P$是$\triangle ABC$的外心,则点$C$的坐标为.
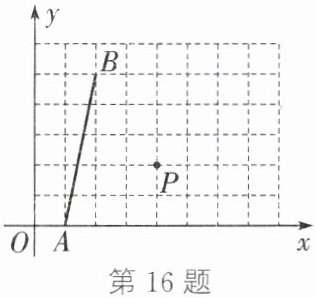

答案:
(6,5),(7,4)
17. (5分)若$\odot O$的半径$r$为4,圆心到直线$l$的距离为$d$,$d$是方程$x^{2}-2x-5=0$的根,请指出直线$l$与$\odot O$的位置关系,并说明理由.
答案:
解方程$x^{2}-2x-5=0$,得$x = \frac{2\pm\sqrt{(-2)^2 - 4×1×(-5)}}{2×1} = 1\pm\sqrt{6}$。
因为距离$d\geq0$,$1 - \sqrt{6}\approx1 - 2.45=-1.45<0$(舍去),所以$d = 1+\sqrt{6}\approx1 + 2.45=3.45$。
已知$\odot O$半径$r = 4$,因为$d\approx3.45<r = 4$,所以直线$l$与$\odot O$相交。
结论:直线$l$与$\odot O$相交。
因为距离$d\geq0$,$1 - \sqrt{6}\approx1 - 2.45=-1.45<0$(舍去),所以$d = 1+\sqrt{6}\approx1 + 2.45=3.45$。
已知$\odot O$半径$r = 4$,因为$d\approx3.45<r = 4$,所以直线$l$与$\odot O$相交。
结论:直线$l$与$\odot O$相交。
查看更多完整答案,请扫码查看


