《2025年5年中考3年模拟七年级数学下册冀教版》

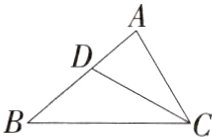
1. 如图,三角形的个数为　　　　　　　　(　　　)
　　　　　　　
　
A.1　　　
　B.2　　　
　C.3　　　
　D.4

答案： 题图中有△ADC,△ABC,△DBC,共3个.故选C.

2. (2024 河北保定竞秀期中)以下列数值为长度的各组线段中,能构成三角形的是　　　　(　　　)
　
A.2,3,7　　　　　　　B.5,8,2
　
C.4,5,6　　　　　　　D.3,3,6

答案： 2+3＜7,故A不能构成三角形;2+5＜8,故B不能构成三角形;4+5＞6,故C能构成三角形;3+3=6,故D不能构成三角形.故选C.

3. 新独家原创 ∠DAC 是△ABC 的一个外角,且∠DAC = 95°,2∠B = 3∠C,则∠B 的度数为
　　　　　　　　　　　　　　　(　　　)
　
A.38°　　　　　　　　B.39°
　
C.52°　　　　　　　　D.57°

答案： 设∠C=x,则∠B=$\frac{3}{2}$∠C=$\frac{3}{2}$x,
∵∠DAC是△ABC的外角，
∴∠DAC=∠B+∠C=$\frac{3}{2}$x+x=95°,解得x=38°,
∴∠B=$\frac{3}{2}$x=$\frac{3}{2}$×38°=57°,故选D.

4. 下列说法:(1)等边三角形是等腰三角形;
　(2)三角形按边的相等关系分类可分为等腰三角形、等边三角形和不等边三角形;(3)三角形按角的大小分类可分为锐角三角形、直角三角形和钝角三角形.其中正确的有　　　　(　　　)
　
A.1 个　　　　　　　　B.2 个
　
C.3 个　　　　　　　　D.0 个

答案：
(1)等边三角形是特殊的等腰三角形，故原说法正确;
(2)三角形按边分类可分为三边互不相等的三角形和等腰三角形，故原说法错误;
(3)三角形按角分类应分为锐角三角形、直角三角形和钝角三角形，故原说法正确.所以正确的说法有2个.故选B.

5. (2024 重庆育才中学模拟)如图,在△ABC 中,AD 是高,AE 是角平分线,AF 是中线,则下列说法中,错误的是　　　　　　　　　　　　(　　　)
　　　　　　
　
A.BF = CF
　
B.∠C + ∠CAD = 90°
　
C.∠BAF = ∠CAF
　
D.S△ABC = 2S△ABF

答案：
∵AF是△ABC的中线,
∴BF=CF,故A说法正确;
∵AD是△ABC的高，
∴∠ADC=90°,
∴∠C+∠CAD =90°,故B说法正确;
∵AE是△ABC的角平分线，
∴∠BAE=∠CAE,而∠BAF与∠CAF不一定相等,故C说法错误;
∵BF=CF,
∴$S_{\triangle ABC}=2S_{\triangle ABF}$,故D说法正确.故选C.

6. (2024 河北石家庄平山月考)如图,在△ABC 中,边
AB 上的高是　　　　　　　　　　　　(　　　)
　　　　　　　
　
A.AF　　　　　　　　B.BE
　
C.CE　　　　　　　　D.BD

答案：

7. (2024 山东临沂期末)如图,在 Rt△ABC 中,∠B =
　90°,∠CED = ∠A,则△CDE 为　　　　(　　　)
　　　　　　　　
　
A.锐角三角形
　
B.直角三角形
　
C.钝角三角形
　
D.以上均有可能

答案：
∵在Rt△ABC中,∠B=90°,
∴∠A+∠C=90°,
∵∠CED=∠A,
∴∠CED+∠C=90°,
∴∠CDE=90°,
∴△CDE为直角三角形,故选B.

8. (2024 河北邢台内丘期末)如图,在锐角三角形
ABC 中,P 是边 AB 上的动点(不与 A,B 重合)，连接 CP,关于①②,下列判断正确的是(　　　)
　①当 P 为 AB 的中点时,△APC 与△PBC 的面积相等;
　②线段 CP 可以把△ABC 分成两个钝角三角形.
　　　　　　　
　
A.只有①正确
　
B.只有②正确
　
C.①②都正确
　
D.①②都不正确

答案：
①如图,过点C作CD⊥AB于点D.

当P为AB的中点时,AP=BP,
∵$S_{\triangle APC}=\frac{1}{2}AP\cdot CD$,$S_{\triangle PBC}=\frac{1}{2}BP\cdot CD$,
∴$S_{\triangle APC}=S_{\triangle PBC}$,
∴①正确.
②
∵△ABC是锐角三角形,
∴∠A＜90°,∠B＜90°,∠ACB＜90°,
∴∠ACP＜∠ACB＜90°,∠BCP＜∠ACB＜90°,
∵∠APC+∠BPC=180°,
∴当∠APC＞90°时,∠BPC＜90°,
当∠BPC＞90°时,∠APC＜90°,
∴∠APC与∠BPC不能同时大于90°,
∴线段CP不可以把△ABC分成两个钝角三角形,
∴②不正确.故选A.