第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
10.(2021河北中考,13,)定理:三角形的一个外角等于与它不相邻的两个内角之和.
已知:如图,∠ACD是△ABC的外角.
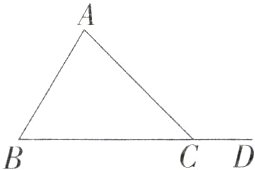
求证:∠ACD = ∠A + ∠B.
|证法1|∵ ∠A + ∠B + ∠ACB = 180°(三角形内角和定理),∠ACD + ∠ACB = 180°(平角定义),∴ ∠ACD + ∠ACB = ∠A + ∠B + ∠ACB(等量代换),∴ ∠ACD = ∠A + ∠B(等式的性质).|
|证法2|∵ ∠A = 76°,∠B = 59°,∠ACD = 135°(量角器测量所得),且135° = 76° + 59°(计算所得),∴ ∠ACD = ∠A + ∠B(等量代换).|
下列说法正确的是 ( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
已知:如图,∠ACD是△ABC的外角.

求证:∠ACD = ∠A + ∠B.
|证法1|∵ ∠A + ∠B + ∠ACB = 180°(三角形内角和定理),∠ACD + ∠ACB = 180°(平角定义),∴ ∠ACD + ∠ACB = ∠A + ∠B + ∠ACB(等量代换),∴ ∠ACD = ∠A + ∠B(等式的性质).|
|证法2|∵ ∠A = 76°,∠B = 59°,∠ACD = 135°(量角器测量所得),且135° = 76° + 59°(计算所得),∴ ∠ACD = ∠A + ∠B(等量代换).|
下列说法正确的是 ( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
答案:
B
∵证法1按照定理证明的一般步骤,从已知出发,经过严谨的推理论证,得出结论正确,具有一般性,无需再证明其他形状的三角形,
∴A的说法不正确,不符合题意,B的说法正确,符合题意.
∵定理的证明必须经过严谨的推理论证,不能用特殊情形来说明,且与测量次数无关,
∴C的说法不正确,不符合题意,D的说法不正确,不符合题意.
∵证法1按照定理证明的一般步骤,从已知出发,经过严谨的推理论证,得出结论正确,具有一般性,无需再证明其他形状的三角形,
∴A的说法不正确,不符合题意,B的说法正确,符合题意.
∵定理的证明必须经过严谨的推理论证,不能用特殊情形来说明,且与测量次数无关,
∴C的说法不正确,不符合题意,D的说法不正确,不符合题意.
11.(2023湖北十堰中考,13,)一副三角尺按如图所示的方式放置,点A在DE上,点F在BC上,若∠EAB = 35°,则∠DFC = ________.
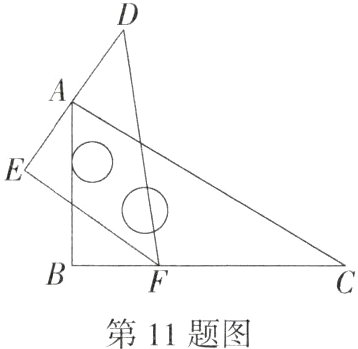

答案:
答案 100°
解析 如图,假设AC与DF相交于点G,
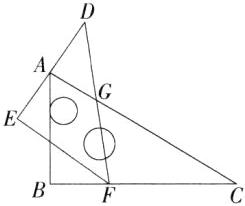
由题意得∠BAC = 60°,∠C = 30°,∠D = 45°,
∵∠EAB = 35°,
∴∠CAD = 180° - ∠EAB - ∠BAC = 85°,
∴∠AGD = 180° - ∠D - ∠CAD = 50°,
∴∠CGF = ∠AGD = 50°,
∴∠DFC = 180° - ∠C - ∠CGF = 100°.
答案 100°
解析 如图,假设AC与DF相交于点G,

由题意得∠BAC = 60°,∠C = 30°,∠D = 45°,
∵∠EAB = 35°,
∴∠CAD = 180° - ∠EAB - ∠BAC = 85°,
∴∠AGD = 180° - ∠D - ∠CAD = 50°,
∴∠CGF = ∠AGD = 50°,
∴∠DFC = 180° - ∠C - ∠CGF = 100°.
12.新考向·规律探究试题 (2024四川达州中考,14,)如图,在△ABC中,AE₁,BE₁分别是内角∠CAB,外角∠CBD的三等分线,且∠E₁AD = $\frac{1}{3}$∠CAB,∠E₁BD = $\frac{1}{3}$∠CBD,在△ABE₁中,AE₂,BE₂分别是内角∠E₁AB,外角∠E₁BD的三等分线,且∠E₂AD = $\frac{1}{3}$∠E₁AB,∠E₂BD = $\frac{1}{3}$∠E₁BD,……,以此规律作下去,若∠C = m,则∠Eₙ的度数为______.
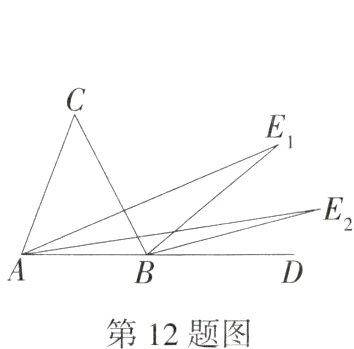

答案:
答案 $\frac{m}{3^{n}}$
解析 ∠E₁ = ∠E₁BD - ∠E₁AD
= $\frac{1}{3}$∠CBD - $\frac{1}{3}$∠CAB
= $\frac{1}{3}$∠C = $\frac{m}{3}$.
同理可得∠E₂ = $\frac{1}{3^{2}}$∠C = $\frac{m}{3^{2}}$,
∴∠Eₙ = $\frac{1}{3^{n}}$∠C = $\frac{m}{3^{n}}$.
解析 ∠E₁ = ∠E₁BD - ∠E₁AD
= $\frac{1}{3}$∠CBD - $\frac{1}{3}$∠CAB
= $\frac{1}{3}$∠C = $\frac{m}{3}$.
同理可得∠E₂ = $\frac{1}{3^{2}}$∠C = $\frac{m}{3^{2}}$,
∴∠Eₙ = $\frac{1}{3^{n}}$∠C = $\frac{m}{3^{n}}$.
13.(2024江苏徐州期中,22,)如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.(M7210002)
(1)若∠B = 40°,∠E = 25°,求∠BAC的度数.
(2)探究∠BAC,∠B,∠E的关系,并说明理由.
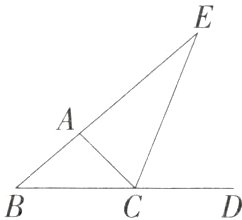
(1)若∠B = 40°,∠E = 25°,求∠BAC的度数.
(2)探究∠BAC,∠B,∠E的关系,并说明理由.

答案:
解析
(1)
∵∠B = 40°,∠E = 25°,
∴∠DCE = ∠B + ∠E = 65°,
∵CE平分∠ACD,
∴∠ACD = 2∠DCE = 130°,
∴∠ACB = 180° - 130° = 50°,
∴∠BAC = 180° - ∠B - ∠ACB = 90°.
(2)∠BAC = ∠B + 2∠E.
理由:
∵CE平分∠ACD,
∴∠DCE = ∠ACE,
∵∠BAC = ∠E + ∠ACE,
∴∠BAC = ∠E + ∠DCE,
∵∠DCE = ∠B + ∠E,
∴∠BAC = ∠E + ∠B + ∠E,
∴∠BAC = ∠B + 2∠E.
(1)
∵∠B = 40°,∠E = 25°,
∴∠DCE = ∠B + ∠E = 65°,
∵CE平分∠ACD,
∴∠ACD = 2∠DCE = 130°,
∴∠ACB = 180° - 130° = 50°,
∴∠BAC = 180° - ∠B - ∠ACB = 90°.
(2)∠BAC = ∠B + 2∠E.
理由:
∵CE平分∠ACD,
∴∠DCE = ∠ACE,
∵∠BAC = ∠E + ∠ACE,
∴∠BAC = ∠E + ∠DCE,
∵∠DCE = ∠B + ∠E,
∴∠BAC = ∠E + ∠B + ∠E,
∴∠BAC = ∠B + 2∠E.
14.推理能力 如图,∠B = 90°,△ABC两外角的平分线交于点D,求∠D的度数.(M7210002)


答案:
解析 由题意知∠B = 90°,∠1 = ∠2,∠3 = ∠4,
∴∠2 = $\frac{1}{2}$(∠B + ∠ACB),∠3 = $\frac{1}{2}$(∠B + ∠BAC),
∴∠2 + ∠3 = $\frac{1}{2}$(∠B + ∠ACB + ∠B + ∠BAC) = $\frac{1}{2}$×(180° + 90°) = 135°,
在△ACD中,∠D = 180° - (∠2 + ∠3) = 180° - 135° = 45°. 故∠D的度数为45°.
∴∠2 = $\frac{1}{2}$(∠B + ∠ACB),∠3 = $\frac{1}{2}$(∠B + ∠BAC),
∴∠2 + ∠3 = $\frac{1}{2}$(∠B + ∠ACB + ∠B + ∠BAC) = $\frac{1}{2}$×(180° + 90°) = 135°,
在△ACD中,∠D = 180° - (∠2 + ∠3) = 180° - 135° = 45°. 故∠D的度数为45°.
查看更多完整答案,请扫码查看


