《2025年5年中考3年模拟七年级数学下册冀教版》

10. 跨语文·《赤壁赋》（2024 河北邯郸丛台模拟）《赤壁赋》：“寄蜉蝣于天地，渺沧海之一粟。”比喻非常渺小。据测量，200 粒粟的质量大约为 1 克，用科学记数法表示一粒粟的质量约为（ ）
A. $2×10²$克
B. $2×10^{-2}$克
C. $5×10^{-2}$克
D. $5×10^{-3}$克

答案： D 1÷200 = 0.005 = 5×10⁻³(克),故选D.

11. 新独家原创 如图，将$\triangle ABC$沿$BA$方向平移 2 $cm$至$\triangle A′B′C′$，且$AA′ = 2AB′$，若图中阴影部分的周长为 12 $cm$，则$\triangle ABC$的周长为（ ）

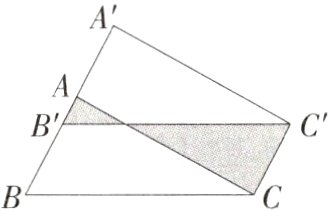
A. 10 $cm$
B. 12 $cm$
C. 15 $cm$
D. 17 $cm$

答案： B
∵△ABC沿BA方向平移2cm得到△A'B'C',
∴BC = B'C',
∴AA' = CC' = BB' = 2cm,
∵AA' = 2AB',
∴AB' = 1cm,
∵图中阴影部分的周长为12cm,
∴AB'+CC'+B'C'+AC = AB + BC + AC = 12cm,
∴△ABC的周长为12cm. 故选B.

12. （2024 河北邢台威县三中月考）一次数学活动中，检验两条纸带①②的边线是否平行，嘉嘉和淇淇采用两种不同的方法：嘉嘉将纸带①沿$AB$折叠，量得$∠1 = ∠2 = 59°$；淇淇将纸带②沿$CD$折叠，发现$CN$与$CM$重合，$DQ$与$DP$重合（点$C$在$MN$上，点$D$在$PQ$上），如图所示，下列判断正确的是（ ）

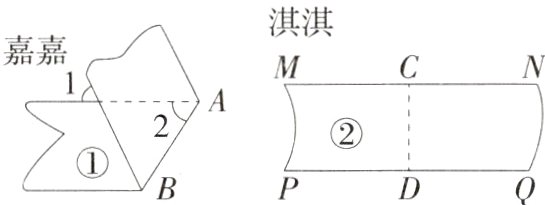
A. 只有纸带①的边线平行
B. 只有纸带②的边线平行
C. 纸带①②的边线都平行
D. 纸带①②的边线都不平行

答案：
B 如图,

∵∠1 = ∠2 = 59°,
∴∠3 = ∠2 = 59°,
∴∠5 = 180° - 59° - 59° = 62°,由折叠知∠4 = ∠5,
∴∠4 = ∠5 = 62°,
∴∠2≠∠4,
∴纸带①的边线不平行;
如题图2,
∵将纸带沿CD折叠,CN与CM重合,DQ与DP重合,
∴∠MCD = ∠NCD = 90°,∠PDC = ∠QDC = 90°,
∴∠MCD + ∠PDC = 180°,
∴纸带②的边线平行. 故选B.

13. （2024 河北沧州沧县期中）若$3ˣ·3ʸ = 3$，则$x + y =$____。

答案： 答案 1
解析
∵3ˣ·3ʸ = 3,
∴3ˣ⁺ʸ = 3,
∴x + y = 1.

14. （2024 河北石家庄四十中期中）若$x - m$与$3 - x$的乘积中不含$x$的一次项，则有理数$m$的值为____。

答案： 答案 -3
解析 (x - m)(3 - x)=3x - x² - 3m + mx=-x²+(3 + m)x - 3m,
∵x - m 与3 - x的乘积中不含x的一次项,
∴3 + m = 0,解得m = -3.

15. （2023 黑龙江鸡西期中）如图，在三角形$ABC$中，$∠ACB = 90°$，$AC = 6$，$BC = 8$，$AB = 10$，$P$为直线$AB$上一动点，连接$PC$，则线段$PC$长度的最小值是____，理由是____。

答案： 答案 24/5;垂线段最短
解析 在三角形ABC中,∠ACB = 90°,AC = 6,BC = 8,AB = 10,
当PC⊥AB时,PC的长度最小(垂线段最短),
此时1/2AB·PC = 1/2AC·BC,
∴PC = 24/5.

16. 河北常考·双空填空题（2024 河北廊坊安次月考）下列各图中的$MA₁$与$NAₙ$平行。
　　
　　
图 1 中的$∠A₁ + ∠A₂ = 180°$，图 2 中的$∠A₁ + ∠A₂ + ∠A₃ = 360°$，图 3 中的$∠A₁ + ∠A₂ + ∠A₃ + ∠A₄ =$____，第$n$个图中的$∠A₁ + ∠A₂ + ∠A₃ + … + ∠Aₙ =$____。

答案： 答案 540°;180°(n - 1)
解析
∵∠A₁ + ∠A₂ = 180°×1,∠A₁ + ∠A₂ + ∠A₃ = 360° = 2×180°,
∴∠A₁ + ∠A₂ + ∠A₃ + ∠A₄ = 3×180° = 540°,
∠A₁ + ∠A₂ + ∠A₃ + … + ∠Aₙ = 180°(n - 1).

17. [答案含评分细则]（2024 江苏泰州期末）（6 分）计算：
(1) $(3 - π)⁰ - (-1)^{2024} + (-\frac{1}{2})^{-2}$。
(2) $x·x⁵ + (-2x²)³ + x⁹÷x³$。

答案： 解析
(1)(3 - π)⁰-(-1)²⁰²⁴+(-1/2)⁻²
=1 - 1 + 4
=4.
(2)x·x⁵+(-2x²)³+x⁹÷x³
=x⁶ - 8x⁶ + x⁶
=-6x⁶.