《2025年亮点给力提优课时作业本五年级数学下册苏教版》

1. 计算涂色部分的周长。
　　

答案：
(1) $(5 + 5)×4 + 3.14×5×2 = 71.4(dm)$
(2) $(15 + 12)×2 = 54(cm)$

2. 计算涂色部分的面积。
　　(1)

答案：
(1) $5×10 = 50(cm^{2})$
(2) $8÷2÷2 = 2(cm)$
$3.14×2^{2}×2 = 25.12(cm^{2})$

3. (1) 观察下面每个图形中小正方形的排列规律，并填空。
　　　　　　　　　　
　　　　　　　　$1 + 2 + 1 = 4 = 2×2$
　　　　　　　　　　
　　　　　　$1 + 2 + 3 + 2 + 1 = 9 = 3×3$
　　　　　　　　　
　　　$1 + 2 + 3 + 4 + 3 + 2 + 1 = (　　　) = (　　　)×(　　　)$
(2) 根据上面的规律，用简便方法计算：
$1 + 2 + 3 + 4 + \cdots + 98 + 99 + 100 + 99 + 98 + \cdots + 4 + 3 + 2 + 1$

答案：
(1) 16 4 4
(2) 原式$ = 100×100 = 10000$

4. 如图，正方形中三个涂色图形周长的和是60厘米，用多少个这样的正方形刚好可以拼成一个面积是9平方分米的长方形？
　　
　　

答案： $60÷4 = 15$(厘米) 9平方分米$ = 900$平方厘米 $900÷(15×15) = 4$(个)

5. 新素养 推理意识 王阿姨卖一筐鸡蛋，第一次卖了全部的一半，第二次卖了余下的一半，第三次卖了第二次余下的一半，第四次卖了第三次余下的一半多4个，这时，鸡蛋全部都卖完了。这筐鸡蛋原来有多少个？

答案： 第三次卖蛋后余下的鸡蛋：$2×4 = 8$(个)
第二次卖蛋后余下的鸡蛋：$2×8 = 16$(个)
第一次卖蛋后余下的鸡蛋：$2×16 = 32$(个)
原有鸡蛋：$2×32 = 64$(个)

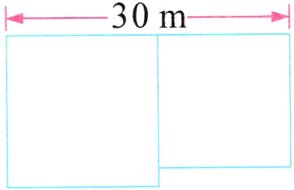
6. 如图，两个正方形的面积相差60平方米，较大的正方形面积是多少平方米？
　　

答案：
$60÷30 = 2$(米) $(30 + 2)÷2 = 16$(米) $16×16 = 256$(平方米) 解析 如图，把相差的面积分成$S_{1}$和$S_{2}$两个长方形的面积，它们的宽是相同的，都是两个正方形的边长差，又因为$S_{1}$等于小正方形的边长乘两个正方形的边长差，且$S_{3}$也等于小正方形的边长乘两个正方形的边长差，所以$S_{3}$和$S_{1}$的面积相等，即相差的部分转化为长为30米的长方形，$60÷30 = 2$(米)，故两个正方形的边长差为2米，边长和为30米，故大正方形的边长为$(30 + 2)÷2 = 16$(米)，大正方形的面积为$16×16 = 256$(平方米)。

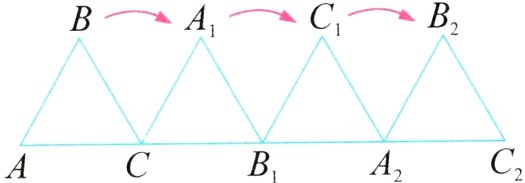
7. 新素养 空间观念 等边三角形ABC的边长是6厘米，现将三角形ABC沿着一条直线翻转三次(如图)，点A经过的路线的长度是多少厘米？
　　　　　　　

答案：
$2×3.14×6÷3×2 = 25.12$(厘米)
解析 如图，第一次翻转，点A经过的路线是以点C为圆心、圆心角为$120^{\circ}$的弧；第二次翻转，点A经过的路线是以点$B_{1}$为圆心、圆心角为$120^{\circ}$的弧；第三次翻转，点A不动。所以翻转三次，点A经过的路线的长度是半径为6厘米的圆周长的$120^{\circ}×2÷360^{\circ}=\frac{2}{3}$，即$2×3.14×6÷3×2 = 25.12$(厘米)。