《2025年亮点给力提优课时作业本五年级数学下册苏教版》

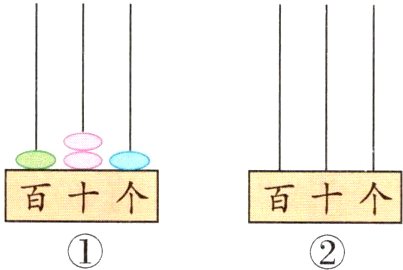
1.（苏州市常熟）在①号计数器上至少再添上(　　　)颗算珠就能拨出3的倍数。在②号计数器上用3颗算珠表示三位数，其中5的倍数共有(　　　)个。
　　　　

答案： 2 3

2.（徐州市睢宁）一个长方形的长是奇数，宽是偶数，周长是(　　　)数，面积是(　　　)数。（填“奇”或“偶”）

答案： 偶 偶

3.（淮安市淮安区）德国数学家哥德巴赫提出猜想：“所有大于2的偶数，都可以表示为两个质数的和。”例如：8 = 5 + 3，请写出符合这个猜想的式子：22 = (　　　)+(　　　)。我国数学家陈景润在猜想证明上取得重大突破，他证明了：“任何足够大的偶数都可以表示成两个质数乘积与一个质数之和。”例如：18 = 3×5 + 3，国际上称“陈氏定理”，请你再写出一个符合“陈氏定理”的式子：(　　　)=(　　　)×(　　　)+(　　　)。

答案： 答案不唯一，如：3 19 24 = 2×11 + 2

4.（扬州市高邮）某小学五年级的学生排队，若每行站15人，少4人；若每行站18人，也少4人。五年级的人数在300到400之间，五年级有(　　　)人。

答案： 356

5.（常州市溧阳）有两个连续的偶数a和b（a、b都大于0），它们的最大公因数是(　　　)。
A. 1
B. 2
C. a
D. $\frac{1}{2}ab$

答案： B

6.（南京市江北新区）下面说法中，正确的是(　　　)。
① 2的倍数一定是偶数，也一定是合数。
② 一个数的倍数，可能是它的因数。
③ 两个数的公倍数的个数是有限的。
④ 如果$x^{2}=2x$，那么x一定是2。
⑤ 1是所有自然数(0除外)的因数。
⑥ 两个奇数的积加上一个偶数，和是奇数。
A. ①②⑤
B. ②④⑤
C. ②⑤⑥
D. ④⑤⑥

答案： C

7.（南京市江宁区）劳动技能大赛上，低年级举行了小巧手叠衣服比赛，共准备了200件外套和280条裤子，每名学生分到的外套数量相同，裤子数量也相同，且没有剩余。最多有多少名学生参赛？每名学生最少叠多少件衣服？

答案： (200,280)=40 最多有40名学生参赛。(200 + 280)÷40 = 12(件) 每名学生最少叠12件衣服。

8.（淮安市洪泽区）为了做好城市亮化工程，有一条路原来从右侧一端起每隔9米有一盏路灯(两端都有)，共有81盏。现在要重新安装，要从右侧一端起每隔6米装一盏。为节省施工成本，有些位置的路灯是不需要重新安装的。不需要重新安装的路灯有多少盏？

答案： 81 - 1 = 80(个) 80×9 = 720(米)
[9,6]=18 720÷18 + 1 = 41(盏)