《2025年亮点给力提优课时作业本五年级数学下册苏教版》

1. 下面各圆中的涂色部分，哪个是扇形？在括号里画“√”。
　　
（ ）（ ）（ ）（ ）

答案： ( )( )( )(√)

2. 填一填。
（1）扇形是由圆的两条（ 　　　　 ）和圆上的一段（ 　　　　 ）围成的，圆心角的顶点在（ 　　　　 ）。
（2）扇形有（ 　　　 ）条对称轴。
（3）把一个圆分成两个扇形，其中大扇形的圆心角的度数是小扇形的5倍。小扇形的圆心角是（ 　　　 ）°，大扇形占整个圆的$\frac{（ 　　　　　　 ）}{（ 　　　　　　 ）}$。
（4）一个钟面上的时针长6厘米，分针长10厘米，从2：45到3：05，分针扫过的区域可以看作扇形。这个扇形的圆心角是（ 　　　 ）°，半径是（ 　　　 ）厘米。

答案：
(1) 半径 曲线 圆心
(2) 1
(3) 60 $\frac{5}{6}$
(4) 120 10

3. 先画一个半径是1.5 cm的圆，再在圆中画一个圆心角是120°的扇形，并用O、r和∠AOB分别表示出圆心、半径和圆心角。

答案：

4. （亮点原创）王叔叔早上出门前看到钟面上的时间是9：30，晚上回到家看到钟面上的时间是5：30，在这段时间内，时针扫过的部分形成的扇形的圆心角是（ 　　　 ）°。

答案： 240

5. （新素养 几何直观）写出下面每个扇形（涂色部分）的圆心角度数和半径。
　　　　　　　　圆心角为（ 　　　 ）°，
　
　半径为（ 　　　 ）cm。
　　　　　　　圆心角为（ 　　　 ）°，
　　　　　　　半径为（ 　　　 ）cm。

答案： 45 8 120 3

6. 如图，三个涂色部分的扇形的半径相等，
　　　　　　　　　　　
这三个扇形的圆心角度数之和是（ 　　　 ）°。

答案： 270 解析 观察题图可知，三个扇形的圆心角度数之和是 360° - 90° = 270°。

7. 如图，绿化部门计划在一个圆形草坪区域（圆O）内规划出一个三角形区域AOB种植鲜花供人们观赏，设计要求三角形AOB所在扇形占圆的$\frac{1}{4}$，此时AB的长度正好为6米，三角形区域的面积是多少平方米？

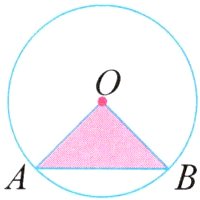
答案： 6×6÷4 = 9(平方米) 解析 由题意可知，三角形 AOB 所在扇形的圆心角是 360°÷4 = 90°，四个三角形 AOB 就可以拼成一个边长为 6 米的正方形，则三角形 AOB 的面积是正方形面积的$\frac{1}{4}$。