第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
8. 甲物体的质量为 2 kg,乙、丙两物体的质量均为 1 kg,三个物体的温度均升高$1℃$,吸收的热量如图 12.3-7 所示。下列说法正确的是(
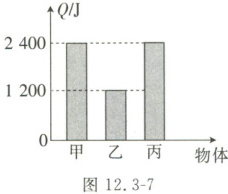
A.甲的比热容比乙的大
B.温度均降低$1℃$时,乙比甲放出的热量多
C.甲的比热容为$2400J/(kg·℃)$
D.甲、丙的比热容之比为$1:2$
D
)
A.甲的比热容比乙的大
B.温度均降低$1℃$时,乙比甲放出的热量多
C.甲的比热容为$2400J/(kg·℃)$
D.甲、丙的比热容之比为$1:2$
答案:
D
9. 图 12.3-8 是用燃气灶烧水的情境和该燃气灶灶头的示意图。

(1)天然气本身无色无味,为了安全,通常会向天然气中加入臭味剂。拧动点火装置,若燃气未点燃,会闻到臭味,表明分子在
(2)拧动点火装置,天然气和空气在进口处混合流向燃烧头并被点燃,天然气不会从进口处外泄,原因是天然气的喷入导致进口处的天然气流速
(3)壶中装有质量为 2 kg 的水,则壶中水的体积为

(1)天然气本身无色无味,为了安全,通常会向天然气中加入臭味剂。拧动点火装置,若燃气未点燃,会闻到臭味,表明分子在
不断地做无规则运动
。(2)拧动点火装置,天然气和空气在进口处混合流向燃烧头并被点燃,天然气不会从进口处外泄,原因是天然气的喷入导致进口处的天然气流速
大
,压强小
。(均选填“大”或“小”)。(3)壶中装有质量为 2 kg 的水,则壶中水的体积为
$2×10^{-3}$
$m^{3}$。若天然气的热值$q = 4.2×10^{7}J/m^{3}$,完全燃烧$1.0×10^{-2}m^{3}$的天然气放出的热量为$4.2×10^{5}$
J,其中$1.68×10^{5}J$的热量被水吸收,水未沸腾,则水的温度升高了20
$℃$。燃气灶的热效率为40%
。
答案:
(1) 不断地做无规则运动
(2) 大;小
(3)
水的体积$V=\frac{m}{\rho}=\frac{2kg}{1.0×10^{3}kg/m^{3}} = 2×10^{-3}m^{3}$
完全燃烧$1.0×10^{-2}m^{3}$天然气放出的热量$Q_{放}=qV = 4.2×10^{7}J/m^{3}×1.0×10^{-2}m^{3}=4.2×10^{5}J$
由$Q_{吸}=cm\Delta t$得,水升高的温度$\Delta t=\frac{Q_{吸}}{cm}=\frac{1.68×10^{5}J}{4.2×10^{3}J/(kg·^{\circ}C)×2kg}= 20^{\circ}C$
燃气灶的热效率$\eta=\frac{Q_{吸}}{Q_{放}}×100\%=\frac{1.68×10^{5}J}{4.2×10^{5}J}×100\% = 40\%$
故答案依次为:
(1)不断地做无规则运动;
(2)大;小;
(3)$2×10^{-3}$;$4.2×10^{5}$;$20$;$40\%$
(1) 不断地做无规则运动
(2) 大;小
(3)
水的体积$V=\frac{m}{\rho}=\frac{2kg}{1.0×10^{3}kg/m^{3}} = 2×10^{-3}m^{3}$
完全燃烧$1.0×10^{-2}m^{3}$天然气放出的热量$Q_{放}=qV = 4.2×10^{7}J/m^{3}×1.0×10^{-2}m^{3}=4.2×10^{5}J$
由$Q_{吸}=cm\Delta t$得,水升高的温度$\Delta t=\frac{Q_{吸}}{cm}=\frac{1.68×10^{5}J}{4.2×10^{3}J/(kg·^{\circ}C)×2kg}= 20^{\circ}C$
燃气灶的热效率$\eta=\frac{Q_{吸}}{Q_{放}}×100\%=\frac{1.68×10^{5}J}{4.2×10^{5}J}×100\% = 40\%$
故答案依次为:
(1)不断地做无规则运动;
(2)大;小;
(3)$2×10^{-3}$;$4.2×10^{5}$;$20$;$40\%$
10. 为了节约能源,很多家庭都安装了太阳能热水器,如图 12.3-9 所示。已知某太阳能热水器储水箱内盛有 50 kg 的水,在阳光照射下,水的温度从$20℃$升高到$59℃$,已知$c_{水}=4.2×10^{3}J/(kg·℃)$。
(1)热水器将太阳能转化为
(2)求水吸收的热量。
(3)这些热量相当于完全燃烧多少煤气放出的热量?($q_{煤气}=3.9×10^{7}J/m^{3}$)

(1)热水器将太阳能转化为
内
能。(2)求水吸收的热量。
(3)这些热量相当于完全燃烧多少煤气放出的热量?($q_{煤气}=3.9×10^{7}J/m^{3}$)

答案:
(1)内
(2)已知:$m = 50\ kg$,$c_{水} = 4.2 × 10^{3}\ J/(kg·℃)$,$t_{0} = 20℃$,$t = 59℃$
$\Delta t = t - t_{0} = 59℃ - 20℃ = 39℃$
$Q_{吸} = c_{水}m\Delta t = 4.2 × 10^{3}\ J/(kg·℃) × 50\ kg × 39℃ = 8.19 × 10^{6}\ J$
(3)已知:$Q_{放} = Q_{吸} = 8.19 × 10^{6}\ J$,$q_{煤气} = 3.9 × 10^{7}\ J/m^3$
由$Q_{放} = Vq$得:$V = \frac{Q_{放}}{q_{煤气}} = \frac{8.19 × 10^{6}\ J}{3.9 × 10^{7}\ J/m^3} = 0.21\ m^3$
(1)内
(2)已知:$m = 50\ kg$,$c_{水} = 4.2 × 10^{3}\ J/(kg·℃)$,$t_{0} = 20℃$,$t = 59℃$
$\Delta t = t - t_{0} = 59℃ - 20℃ = 39℃$
$Q_{吸} = c_{水}m\Delta t = 4.2 × 10^{3}\ J/(kg·℃) × 50\ kg × 39℃ = 8.19 × 10^{6}\ J$
(3)已知:$Q_{放} = Q_{吸} = 8.19 × 10^{6}\ J$,$q_{煤气} = 3.9 × 10^{7}\ J/m^3$
由$Q_{放} = Vq$得:$V = \frac{Q_{放}}{q_{煤气}} = \frac{8.19 × 10^{6}\ J}{3.9 × 10^{7}\ J/m^3} = 0.21\ m^3$
查看更多完整答案,请扫码查看


