《2025年作业本江西教育出版社九年级物理上册沪粤版》

1. 把 1 kg 的水从$60℃$开始加热至沸腾，温度随时间变化的图像如图 12.3-5 所示。水沸腾前，容器内的水温度升高，是通过热传递的方式增加内能的。水沸腾时，水面上方的气压小于(选填“大于”“小于”或“等于”)标准大气压。水从$70℃$加热至$90℃$需要吸收的热量是$8.4×10^{4}$J。$[c_{水}=4.2×10^{3}J/(kg·℃)]$

答案： 热传递， 小于，$ 8.4 × 10^{4}$

2. 水沸腾时如果继续吸热，温度保持不变。灶上的锅中装有 2 kg 初温为$30℃$的水，当水吸收了$7.56×10^{5}J$的热量后，水温升高了70$℃$，末温是100$℃$。(当地为标准大气压)

答案： 保持不变；70；100

3. 火星探测器天问一号的成功发射，是我国综合国力和创新能力提升的重要标志。若搭载天问一号的火箭发射时携带了$3×10^{4}kg$液氢燃料，这些燃料完全燃烧放出的热量是$4.2 × 10^{12}$J，可以将$1.25 × 10^{7}$kg 初温为$20℃$的水加热至沸腾。$[q_{氢}=1.4×10^{8}J/kg，c_{水}=4.2×10^{3}J/(kg·℃)$，当地大气压为标准大气压，不计热量损失]

答案： 一、计算燃料完全燃烧放出的热量：
根据公式：$Q_{放}=m· q$，
已知$m = 3×10^{4}kg$，$q_{氢}=1.4×10^{8}J/kg$，
则$Q_{放}=3×10^{4}kg×1.4×10^{8}J/kg = 4.2×10^{12}J$。
二、计算水的质量：
因为不计热量损失，所以$Q_{吸}=Q_{放}= 4.2×10^{12}J$，
在标准大气压下，水的沸点为$100° C$，则$\Delta t = 100° C - 20° C = 80° C$，
根据公式$Q_{吸}=c_{水}· m·\Delta t$，可得$m_{水}=\frac{Q_{吸}}{c_{水}·\Delta t}$，
已知$c_{水}=4.2×10^{3}J/(kg·° C)$，
则$m_{水}=\frac{4.2×10^{12}J}{4.2×10^{3}J/(kg·° C)×80° C}=1.25×10^{7}kg$。
故答案依次为：$4.2 × 10^{12}$；$1.25 × 10^{7}$。

4. 一保温杯中装有质量为 200 g、温度为$25℃$的水。将一个质量为 100 g、温度为$100℃$的金属块放入杯中，一段时间后杯内水和金属块的温度稳定在$30℃$，则水吸收的热量为4200J。假设金属块放出的热量全部被水吸收，水的比热容为$4.2×10^{3}J/(kg·℃)$，则该金属块的比热容为600$J/(kg·℃)$。

答案： 水的质量$m_{水}=200g=0.2kg$，初温$t_{0水}=25℃$，末温$t=30℃$，水的比热容$c_{水}=4.2×10^{3}J/(kg·℃)$。
水吸收的热量：
$Q_{吸}=c_{水}m_{水}(t - t_{0水})=4.2×10^{3}J/(kg·℃)×0.2kg×(30℃ - 25℃)=4.2×10^{3}×0.2×5J=4200J$。
金属块的质量$m_{金}=100g=0.1kg$，初温$t_{0金}=100℃$，末温$t=30℃$，金属块放出的热量$Q_{放}=Q_{吸}=4200J$。
由$Q_{放}=c_{金}m_{金}(t_{0金}-t)$得，金属块的比热容：
$c_{金}=\frac{Q_{放}}{m_{金}(t_{0金}-t)}=\frac{4200J}{0.1kg×(100℃ - 30℃)}=\frac{4200}{0.1×70}J/(kg·℃)=600J/(kg·℃)$。
4200；600

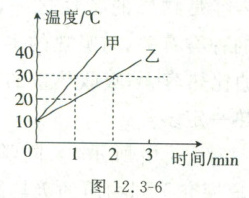
5. 用相同的加热器同时对质量相等的甲、乙两种液体加热（不计热量损失），根据记录的实验数据描绘二者的温度—时间图像，如图 12.3-6 所示。已知乙液体为煤油，$c_{煤油}=2.1×10^{3}J/(kg·℃)$，根据图像可计算出甲物质的比热容为$1.05×10^{3}J/(kg·^{\circ}C)$。

答案： 1. 首先明确热量公式：
根据$Q = cm\Delta t$（$Q$为吸收的热量，$c$为比热容，$m$为质量，$\Delta t$为温度变化量），因为用相同的加热器同时加热，不计热量损失，所以在相同时间内$Q_{甲}=Q_{乙}$，且$m_{甲}=m_{乙}$。
2. 然后从图像获取数据：
取加热时间$t = 2min$，对于甲液体：$\Delta t_{甲}=30^{\circ}C - 10^{\circ}C=20^{\circ}C$；对于乙液体（煤油）：$\Delta t_{乙}=20^{\circ}C - 10^{\circ}C = 10^{\circ}C$。
已知$c_{乙}=c_{煤油}=2.1×10^{3}J/(kg·^{\circ}C)$。
由$Q_{甲}=Q_{乙}$，$m_{甲}=m_{乙}$，根据$Q = cm\Delta t$可得$c_{甲}m_{甲}\Delta t_{甲}=c_{乙}m_{乙}\Delta t_{乙}$。
因为$m_{甲}=m_{乙}$，所以$c_{甲}\Delta t_{甲}=c_{乙}\Delta t_{乙}$。
3. 最后计算甲物质的比热容：
则$c_{甲}=\frac{c_{乙}\Delta t_{乙}}{\Delta t_{甲}}$。
把$c_{乙}=2.1×10^{3}J/(kg·^{\circ}C)$，$\Delta t_{乙}=10^{\circ}C$，$\Delta t_{甲}=20^{\circ}C$代入上式，可得$c_{甲}=\frac{2.1×10^{3}J/(kg·^{\circ}C)×10^{\circ}C}{20^{\circ}C}=1.05×10^{3}J/(kg·^{\circ}C)$。
故答案为：$1.05×10^{3}J/(kg·^{\circ}C)$。

6. 铜、铅的比热容之比是$3:1$，一铜块和一铅块的质量之比是$2:3$，若它们吸收的热量相同，升高的温度之比是1:2，升温后铜与铅的比热容之比是3:1。

答案： 已知：$c_{铜}:c_{铅} = 3:1$，$m_{铜}:m_{铅} = 2:3$，$Q_{铜} = Q_{铅} = Q$。
由热量公式$Q = cm\Delta t$得$\Delta t=\frac{Q}{cm}$。
$\Delta t_{铜}:\Delta t_{铅}=\frac{Q}{c_{铜}m_{铜}}:\frac{Q}{c_{铅}m_{铅}}=\frac{c_{铅}m_{铅}}{c_{铜}m_{铜}}=\frac{1×3}{3×2}=\frac{1}{2}=1:2$。
比热容是物质的特性，与温度无关，故升温后$c_{铜}:c_{铅} = 3:1$。
1:2；3:1

7. 把质量为 50 g、初温为$90℃$的热水与质量为 90 g、初温为$20℃$的冷水混合成温水，不计热量损失，温水的温度为(B)

A.$30℃$
B.$45℃$
C.$55℃$
D.$5℃$

答案： B