《2026年秒杀中考数学安徽专版》

10. 如图,在$Rt\triangle ABC$中,$\angle ABC=90^{\circ}$,$AB=4$,$BC=2$,$BD$是边$AC$上的高.点$E$,$F$分别在边$AB$,$BC$上(不与端点重合),且$DE\perp DF$.设$AE=x$,四边形$DEBF$的面积为$y$,则$y$关于$x$的函数图象为(A)


A.图A
B.图B
C.图C
D.图D

答案：
10.A 【解析】本题考查函数图象的识别，相似三角形的判定以及性质.
如图，过点E作EH⊥AC于点H.

∵∠ABC = 90°，AB = 4，BC = 2，
∴AC = $\sqrt{AB^{2}+BC^{2}}$ = 2$\sqrt{5}$.
∵BD是边AC上的高，
∴$\frac{1}{2}$AB·BC = $\frac{1}{2}$AC·BD，
∴BD = $\frac{4\sqrt{5}}{5}$.
∵∠BAC = ∠CAB，∠ABC = ∠ADB = 90°，
∴△ABC∽△ADB，
∴$\frac{AB}{AD}$ = $\frac{AC}{AB}$
解得AD = $\frac{8\sqrt{5}}{5}$，
∴DC = AC - AD = 2$\sqrt{5}$ - $\frac{8\sqrt{5}}{5}$ = $\frac{2\sqrt{5}}{5}$.
∵∠BDF + ∠BDE = ∠BDE + ∠EDA = 90°，
∠CBD + ∠DBA = ∠DBA + ∠A = 90°，
∴∠DBC = ∠A，∠BDF = ∠EDA，
∴△AED∽△BFD，
∴$\frac{S_{\triangle AED}}{S_{\triangle BFD}}$ = ($\frac{AD}{BD}$)² = $\frac{(\frac{8\sqrt{5}}{5})^{2}}{(\frac{4\sqrt{5}}{5})^{2}}$ = 4，
∴S△AED = 4S△BFD，作DG⊥AB于点G，则DG =
AD·sinA = $\frac{8\sqrt{5}}{5}$×$\frac{2}{2\sqrt{5}}$ = $\frac{8}{5}$.
∴S四边形DEBF = S△ABC - S△AED - (S△BDC - S△BFD)
= $\frac{1}{2}$×AB×BC - $\frac{1}{2}$×AE×DG - $\frac{1}{2}$×DC×DB + $\frac{1}{4}$S△AED
= $\frac{1}{2}$×4×2 - $\frac{1}{2}$×3×$\frac{8}{5}$ - $\frac{1}{2}$×$\frac{2\sqrt{5}}{5}$×$\frac{4\sqrt{5}}{5}$
= $\frac{16}{5}$ - $\frac{3}{5}$x.
∵0 ＜ x ＜ 4，
∴当x = 0时，S四边形DEBF = $\frac{16}{5}$，
当x = 4时，S四边形DEBF = $\frac{4}{5}$.由图象可知，只有选项A符合题意.
【高分点拨】点拨：几何动点问题的函数图象
1.观察型(函数的图象有明显的增减性差异)：根据题目描述，只需确定函数值在每段函数图象上随着自变量的增减情况或变化的快慢即可得解.
(1)当函数值随着自变量增大而增大时，函数图象呈上升趋势，反之则下降.
(2)当自变量增大，函数值不变时，函数图象与x轴平行.
(3)当自变量不变而函数值变化时，函数图象与y轴平行.
2.计算型：先根据自变量的取值范围对函数进行分段，再求出每段函数的解析式，最后由每段函数的解析式确定每段函数图象的形状.

11. 若代数式$\dfrac{1}{x-4}$有意义,则实数$x$的取值范围是x≠4.

答案： 11.x≠4 【解析】本题考查分式有意义的条件.
∵分式有意义的条件是分母不能等于0，
∴x - 4≠0，
∴x≠4.

12. [数学文化]我国古代数学家张衡将圆周率取值为$\sqrt{10}$,祖冲之给出圆周率的一种分数形式的近似值为$\dfrac{22}{7}$.比较大小:$\sqrt{10}$＞$\dfrac{22}{7}$(选填“$＞$”或“$＜$”).

答案： 12.＞ 【解析】本题考查实数的大小比较.
∵($\frac{22}{7}$)² = $\frac{484}{49}$，($\sqrt{10}$)² = 10 = $\frac{490}{49}$，
而$\frac{484}{49}$ ＜ $\frac{490}{49}$，
∴($\frac{22}{7}$)² ＜ ($\sqrt{10}$)²，
∴$\sqrt{10}$ ＞ $\frac{22}{7}$.

13. 不透明的袋中装有大小质地完全相同的$4$个球,其中$1$个黄球、$1$个白球和$2$个红球.从袋中任取$2$个球,恰为$2$个红球的概率是$\frac{1}{6}$.

答案：
13.$\frac{1}{6}$ 【解析】本题考查用树状图或列表法求概率.画树状图如下：

由树状图可得，共有12种结果，其中恰为2个红球的结果有2种，
∴恰为2个红球的概率为$\frac{2}{12}$ = $\frac{1}{6}$.

14. 如图,现有正方形纸片$ABCD$,点$E$,$F$分别在边$AB$,$BC$上,沿垂直于$EF$的直线折叠得到折痕$MN$,点$B$,$C$分别落在正方形所在平面内的点$B'$,$C'$处,然后还原.
(1) 若点$N$在边$CD$上,且$\angle BEF=\alpha$,则$\angle C'NM=$90°−α(用含$\alpha$的式子表示).
(2) 再沿垂直于$MN$的直线折叠得到折痕$GH$,点$G$,$H$分别在边$CD$,$AD$上,点$D$落在正方形所在平面内的点$D'$处,然后还原.若点$D'$在线段$B'C'$上,且四边形$EFGH$是正方形,$AE=4$,$EB=8$,$MN$与$GH$的交点为点$P$,则$PH$的长为3$\sqrt{5}$.

答案：
14.
(1)90° - α
(2)3$\sqrt{5}$ 【解析】本题考查折叠的性质，相似三角形的判定与性质，勾股定理等知识.
(1)如图，连接CC′.由题意，得∠C′NM = ∠4，
MN⊥CC′.

∵MN⊥EF，
∴CC′//FE，
∴∠1 = ∠2.
∵四边形ABCD是正方形，
∴∠B = ∠BCD = 90°，
∴∠3 + ∠4 = ∠3 + ∠2 = 90°，∠1 + ∠BEF = 90°，
∴∠2 = ∠4，∠1 = 90° - α，
∴∠4 = 90° - α，
∴∠C′NM = 90° - α.
(2)如图，记HG与NC′交于点K.

∵四边形ABCD和四边形EFGH都是正方形，
∴∠A = ∠B = ∠C = ∠D = 90°，HE = FE，
∠HEF = 90°，
∴∠5 + ∠6 = ∠7 + ∠6 = 90°，
∴∠5 = ∠7，
∴△AEH≌△BFE(AAS).
同理可证，△AEH≌△BFE≌△DHG≌△CGF，
∴AE = CG = DH = 4，DG = BE = 8.
在Rt△HDG中，由勾股定理，
得HG = $\sqrt{DH^{2}+DG^{2}}$ = 4$\sqrt{5}$.
由题意，得∠NC′D′ = ∠NCB = 90°，∠8 = ∠9，∠D = ∠GD′H = 90°，NC = NC′，GD = GD′ = 8，
∴NC′//GD′，
∴∠NKG = ∠9，
∴∠8 = ∠NKG，
∴NG = NK，
∴NC - NG = NC′ - NK，
即KC′ = GC = 4.
∵NC′//GD′，
∴△HC′K∽△HD′G，
∴$\frac{HK}{HG}$ = $\frac{C′K}{D′G}$ = $\frac{1}{2}$，
∴HK = $\frac{1}{2}$HG，
∴HK = KG.
由题意，得MN⊥HG，而NG = NK，
∴PK = PG，
∴PH = $\frac{3}{4}$HG = 3$\sqrt{5}$.
【高分点拨】点拨：解决折叠问题的一般思考过程
图形折叠的本质是轴对称，解决折叠问题的关键是寻找图形中相等的线段、角，从而把折叠问题转化为一般问题.一般思考过程如下：
(1)利用轴对称的性质找到折叠前后的不变量与变量.
(2)根据题目中的已知角、线段之间的关系，结合三角形的内角、三角形的内角与外角的关系，把求解的线段或角转移到相应特殊的直角三角形、等腰三角形等中进一步求解.

15. 解方程:$x^{2}-2x=3$.

答案： 15.解：
∵x² - 2x = 3，
∴x² - 2x - 3 = 0，
∴(x - 3)(x + 1) = 0，
∴x₁ = 3，x₂ = - 1.(8分)

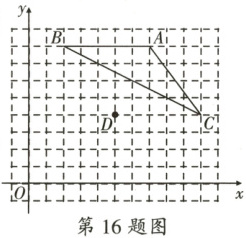
16. 如图,在由边长为$1$个单位长度的小正方形组成的网格中建立平面直角坐标系,格点(网格线的交点)$A$,$B$,$C$,$D$的坐标分别为$(7,8)$,$(2,8)$,$(10,4)$,$(5,4)$.
(1) 以点$D$为旋转中心,将$\triangle ABC$旋转$180^{\circ}$得到$\triangle A_{1}B_{1}C_{1}$,画出$\triangle A_{1}B_{1}C_{1}$.
(2) 直接写出以$B$,$C_{1}$,$B_{1}$,$C$为顶点的四边形的面积.
(3) 所给的网格图中确定一个格点$E$,使得射线$AE$平分$\angle BAC$,写出点$E$的坐标.

答案：
16.解：
(1)如图所示，△A₁B₁C₁即为所求.(3分)

(2)如图，连接BB₁，CC₁.
∵点B与B₁，点C与C₁分别关于点D成中心对称，
∴DB = DB₁，DC = DC₁，
∴四边形BC₁B₁C是平行四边形，
∴S₀BC₁B₁C = 2△CC₁B₁ = 2×$\frac{1}{2}$×10×4 = 40.(6分)
(3)点E(6，6).(答案不唯一)(8分)
【高分点拨】点拨：旋转作图的基本步骤
①确定旋转方向、旋转中心及旋转角度；②找出原图形中的关键点；③确定旋转后的各对应点；④按照原图形顺次连接得到的各对应点，即可得到旋转后的图形.