《2026年秒杀中考数学安徽专版》

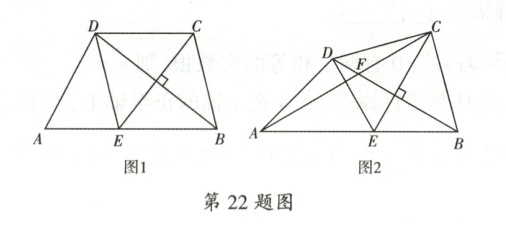
22. 已知在四边形$ABCD$中，$BC = CD$，连接$BD$，过点$C$作$BD$的垂线交$AB$于点$E$，连接$DE$。
（1）如图 1，若$DE // BC$，求证：四边形$BCDE$是菱形。
（2）如图 2，连接$AC$，设$BD$，$AC$相交于点$F$，$DE$垂直平分线段$AC$。
① 求$\angle CED$的大小；
② 若$AF = AE$，求证：$BE = CF$。
 

答案： 22.【解析】本题是四边形综合题，考查了菱形的判定与性质、全等三角形的判定与性质、线段垂直平分线的性质等知识，熟练掌握线段垂直平分线的性质是解题的关键.
(1)利用$AAS$证明$\triangle DOE \cong \triangle BOC$，得$DE = BC$，从而得出四边形$BCDE$是平行四边形，根据$CD = CB$，即可证明结论.
(2)①根据线段垂直平分线的性质，得$AE = EC$且$DE \perp AC$，$\therefore \angle AED = \angle CED$.又$\because CD = CB$且$CE \perp BD$，$\therefore CE$垂直平分$DB$，$\therefore DE = BE$，$\therefore \angle DEC = \angle BEC$，$\therefore \angle AED = \angle CED = \angle BEC$.又$\because \angle AED + \angle CED + \angle BEC = 180^{\circ}$，$\therefore \angle CED = \frac{1}{3} × 180^{\circ} = 60^{\circ}$.
②证明：由①，得$AE = EC$，又$\because \angle AEC = \angle AED + \angle DEC = 120^{\circ}$，$\therefore \angle ACE = 30^{\circ}$.同理可得，在等腰三角形$DEB$中，$\angle EBD = 30^{\circ}$，$\therefore \angle ACE = \angle ABF = 30^{\circ}$.在$\triangle ACE$与$\triangle ABF$中，$\begin{cases} \angle ACE = \angle ABF \\ \angle CAE = \angle BAF \\ AE = AF \end{cases}$，$\therefore \triangle ABF \cong \triangle ACE(AAS)$，$\therefore AC = AB$，又$\because AE = AF$，$\therefore AB - AE = AC - AF$，即$BE = CF$.
【解题过程】
解：
(1)证明：设CE与BD交于点O，$\because CB = CD$，$CE \perp BD$，$\therefore DO = BO$. $\because DE // BC$，$\therefore \angle DEO = \angle BCO$.(1分)又$\because \angle DOE = \angle BOC$，$\therefore \triangle DOE \cong \triangle BOC(AAS)$，$\therefore DE = BC$，$\therefore$四边形$BCDE$是平行四边形.(3分)$\because CD = CB$，$\therefore$平行四边形$BCDE$是菱形.(4分)
(2)①$\because DE$垂直平分$AC$，$\therefore AE = EC$且$DE \perp AC$，$\therefore \angle AED = \angle CED$.(5分)又$\because CD = CB$且$CE \perp BD$，$\therefore CE$垂直平分$DB$，$\therefore DE = BE$，$\therefore \angle DEC = \angle BEC$，$\therefore \angle AED = \angle CED = \angle BEC$.(7分)又$\because \angle AED + \angle CED + \angle BEC = 180^{\circ}$，$\therefore \angle CED = \frac{1}{3} × 180^{\circ} = 60^{\circ}$.(8分)
②证明：由①，得$AE = EC$，又$\because \angle AEC = \angle AED + \angle DEC = 120^{\circ}$，$\therefore \angle ACE = 30^{\circ}$.同理可得，在等腰三角形$DEB$中，$\angle EBD = 30^{\circ}$，$\therefore \angle ACE = \angle ABF = 30^{\circ}$.(9分)在$\triangle ACE$与$\triangle ABF$中，$\begin{cases} \angle ACE = \angle ABF \\ \angle CAE = \angle BAF \\ AE = AF \end{cases}$，$\therefore \triangle ABF \cong \triangle ACE(AAS)$，$\therefore AC = AB$，(11分)又$\because AE = AF$，$\therefore AB - AE = AC - AF$，即$BE = CF$.(12分)
【高分点拨】 点拨：特殊四边形的判定
1.平行四边形的判定
(1)两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)两组对角分别相等的四边形是平行四边形.
(4)对角线互相平分的四边形是平行四边形.
(5)一组对边平行且相等的四边形是平行四边形.
2.矩形的判定
(1)有一个角是直角的平行四边形是矩形.
(2)有三个角是直角的四边形是矩形.
(3)对角线互相平分且相等的四边形是矩形.
3.菱形的判定
(1)有一组邻边相等的平行四边形是菱形.
(2)对角线互相垂直的平行四边形是菱形.
(3)四条边都相等的四边形是菱形.
4.正方形的判定
(1)有一个角是直角的菱形是正方形.
(2)有一组邻边相等的矩形是正方形.
(3)有一组邻边相等，并且有一个角是直角的平行四边形是正方形.
(4)对角线互相垂直的矩形是正方形.
(5)对角线相等的菱形是正方形.
(6)对角线互相垂直平分且相等的四边形是正方形.