《2026年秒杀中考数学安徽专版》

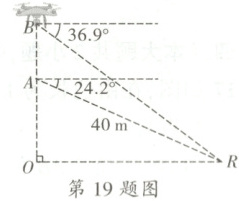
19. 如图，$O$，$R$是同一水平线上的两点，无人机从点$O$竖直上升到点$A$时，测得$A$到点$R$的距离为40 m，点$R$的俯角为$24.2°$，无人机继续竖直上升到点$B$，测得点$R$的俯角为$36.9°$。求无人机从点$A$到点$B$的上升高度$AB$。（结果精确到0.1 m，参考数据：$\sin 24.2° \approx 0.41$，$\cos 24.2° \approx 0.91$，$\tan 24.2° \approx 0.45$，$\sin 36.9° \approx 0.60$，$\cos 36.9° \approx 0.80$，$\tan 36.9° \approx 0.75$）

答案： 19.[解析]本题考查解直角三角形的应用.解Rt$\triangle AOR$，求得$AO$，$RO$，在Rt$\triangle BOR$中，求得$BO$，最后根据$AB = BO - AO$，即可求解.
[解题过程]
解：根据题意，得$\angle ARO = 24.2^{\circ}$，$\angle BRO = 36.9^{\circ}$，$AR = 40$.
在Rt$\triangle AOR$中，$\frac{AO}{AR} = \sin \angle ARO$，
$\frac{RO}{AR} = \cos \angle ARO$，
$\therefore AO = AR · \sin \angle ARO = 40\sin 24.2^{\circ} \approx 16.4(m)$，(4分)
$RO = AR · \cos \angle ARO = 40\cos 24.2^{\circ} \approx 36.4(m)$.(6分)
在Rt$\triangle BOR$中，$\frac{OB}{OR} = \tan \angle BRO$，
$\therefore OB = OR · \tan \angle BRO = 36.4\tan 36.9^{\circ} \approx 27.3(m)$，(8分)
$\therefore AB = OB - AO = 27.3 - 16.4 = 10.9(m)$.
答：无人机从A点到B点的上升高度AB约为10.9 m.(10分)
【高分点拨】 点拨：解直角三角形
1.解直角三角形的实际应用题的解题步骤
(1)审题：结合示意图，弄清楚已知量和未知量.
(2)构造直角三角形：将已知条件转化到示意图中，把实际问题转化为解直角三角形的问题；若已知条件不能在图中体现，则需添加适当的辅助线，高线是常作的辅助线.
(3)列关系式：根据直角三角形边角之间的关系列式求解.
(4)检验：解题完毕后，要特别注意所求结果是否符合实际意义，同时还要注意结果有无对精确度的要求.
2.角的相关概念
概念 定义
仰角、俯角 视线在水平线上方的角叫仰角，视线在水平线下方的角叫俯角
坡度（坡比）、坡角 坡面的垂直高度$h$与水平宽度$l$的比叫坡度（坡比），用字母$i$表示；坡面与水平面的夹角$\alpha$叫坡角，$i = \tan \alpha = \frac{h}{l}$
方向角 一般是指以观测者的位置为中心，将正北或正南方向作为起始方向，旋转到目标的方向线所成的角（一般指锐角），通常表达成北（南）偏东（西）$× ×$度，若正好为$45^{\circ}$，则表示为正西（东）南（北）

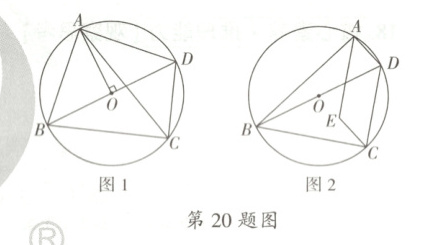
20. 已知四边形$ABCD$内接于$\odot O$，对角线$BD$是$\odot O$的直径。
（1）如图1，连接$OA$，$CA$，若$OA \perp BD$，求证：$CA$平分$\angle BCD$。
（2）如图2，$E$为$\odot O$内一点，满足$AE \perp BC$，$CE \perp AB$，若$BD = 3\sqrt{3}$，$AE = 3$，求弦$BC$的长。

答案： 20.[解析]本题考查圆周角定理、垂径定理、勾股定理、平行四边形的判定与性质.
(1)由垂径定理和圆周角的性质证出$\angle ACB = \angle ACD$，则可得出结论.
(2)根据圆周角定理的推论，得到$DC \perp BC$，$DA \perp AB$，进而$DC // AE$，$DA // CE$，证明四边形AECD是平行四边形，则$AE = CD = 3$，然后根据勾股定理即可得出答案.
[解题过程]
解：
(1)证明：$\because$对角线BD是$\odot O$的直径，$OA \perp BD$，
$\therefore \overset{\frown}{AB} = \overset{\frown}{AD}$，$\therefore \angle ACB = \angle ACD$，
$\therefore CA$平分$\angle BCD$.(4分)
(2)$\because$对角线BD是$\odot O$的直径，
$\therefore \angle BAD = \angle BCD = 90^{\circ}$，(6分)
$\therefore DC \perp BC$，$DA \perp AB$.
$\because AE \perp BC$，$CE \perp AB$，
$\therefore DC // AE$，$DA // CE$，
$\therefore$四边形AECD是平行四边形，(8分)
$\therefore DC = AE = 3$.
又$\because BD = 3\sqrt{3}$，$\therefore BC = \sqrt{(3\sqrt{3})^{2} - 3^{2}} = 3\sqrt{2}$.(10分)

21. 核心素养·数据观念 端午节是中国的传统节日，民间有端午节吃粽子的习俗，在端午节来临之际，某校七、八年级开展了一次“包粽子”实践活动，对学生的活动情况按10分制进行评分，成绩(单位：分)均为不低于6的整数。为了解这次活动的效果，现从这两个年级各随机抽取10名学生的活动成绩作为样本进行整理，并绘制统计图表，部分信息如下：

已知八年级10名学生活动成绩的中位数为8.5分。
请根据以上信息，回答下列问题：
(1)样本中，七年级活动成绩为7分的学生数是1，七年级活动成绩的众数为8分。
(2)$a = $2，$b = $3。
(3)若认定活动成绩不低于9分为“优秀”，根据样本数据，判断本次活动中优秀率高的年级是否平均成绩也高，并说明理由。

答案： 21.[解析]本题考查扇形统计图、统计表、中位数、众数、求一组数据的平均数.
(1)根据扇形统计图得出七年级活动成绩为7分的学生数的占比，即可得出七年级活动成绩为7分的学生数，根据扇形统计图结合众数的定义，即可求解.
(2)根据中位数的定义将八年级的活动成绩从小到大排列，那么其中位数应是第5个和第6个数据的平均数，结合已知条件易得第5个和第6个数据分别为8,9，再根据表格中数据即可求得答案.
(3)结合
(1)
(2)中所求，分别求得两个年级的优秀率和平均成绩后进行比较即可.
[解题过程]
解：
(1)1 8(2分)
(2)2 3(6分)
(3)优秀率高的年级不是平均成绩也高.理由如下：
$\because$七年级优秀率为$20\% + 20\% = 40\%$，平均成绩为$7 × 10\% + 8 × 50\% + 9 × 20\% + 10 × 20\% = 8.5$，(8分)
八年级优秀率为$\frac{3 + 2}{10} × 100\% = 50\% ＞ 40\%$，平均成绩为$\frac{1}{10} × (6 + 7 × 2 + 8 × 2 + 9 × 3 + 10 × 2) = 8.3 ＜ 8.5$，(10分)
$\therefore$优秀率高的年级为八年级，但平均成绩七年级更高，$\therefore$优秀率高的年级不是平均成绩也高.(12分)