第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
8. 已知一次函数$y = k_{1}x + m$与反比例函数$y = \dfrac{k_{2}}{x}$的图象交于$A(1, -2)$,$B(n, 4)$两点,当一次函数的值小于反比例函数的值时,$x$的取值范围是(
A.$x > 1$或$x < -\dfrac{1}{2}$
B.$x < -\dfrac{1}{2}$或$0 < x < 1$
C.$x > 1$或$-\dfrac{1}{2} < x < 0$
D.$0 < x < 1$或$-\dfrac{1}{2} < x < 0$
C
)A.$x > 1$或$x < -\dfrac{1}{2}$
B.$x < -\dfrac{1}{2}$或$0 < x < 1$
C.$x > 1$或$-\dfrac{1}{2} < x < 0$
D.$0 < x < 1$或$-\dfrac{1}{2} < x < 0$
答案:
8.C
9. 在凸五边形$ABCDE$中,点$P$在边$BC$上,点$Q$在$AD$的延长线上,$AQ$与$BC$平行且相等,不能推出$PA$与$CD$一定平行的是(
A.$PB = QD$
B.$PA = CD$
C.$\angle BAP = \angle DCQ$
D.$\angle APB = \angle CDQ$
B
)A.$PB = QD$
B.$PA = CD$
C.$\angle BAP = \angle DCQ$
D.$\angle APB = \angle CDQ$
答案:
9.B 【解析】如图.

∵AQ = BC,AQ//BC,
∴四边形ABCQ是平行四边形,
∴AB//CQ,∠BAQ = ∠BCQ.
A:
∵PB = QD,
∴AQ−DQ = BC−BP,即AD = CP.
∵AQ//BC,
∴四边形APCD是平行四边形,
∴PA//CD,故选项A正确,不符合题意;
B:
∵PA = CD,如图:

四边形APCD可能是等腰梯形,
∴不能推出PA与CD一定平行,故选项B错误,符合题意;
C:
∵∠BAP = ∠DCQ,
∴∠BAQ−∠BAP = ∠BCQ−∠DCQ,
即∠PAQ = ∠BCD.
∵AQ//BC,
∴∠PAQ + ∠APC = ∠BCD + ∠ADC = 180°,
∴∠APC = ∠ADC,
∴∠PAQ + ∠ADC = 180°,
∴PA//CD,故选项C正确,不符合题意;
D:
∵∠APB = ∠CDQ,
∴∠APC = ∠ADC,
同理C选项,得∠PAQ + ∠ADC = 180°,
∴PA//CD,故选项D正确,不符合题意.
9.B 【解析】如图.

∵AQ = BC,AQ//BC,
∴四边形ABCQ是平行四边形,
∴AB//CQ,∠BAQ = ∠BCQ.
A:
∵PB = QD,
∴AQ−DQ = BC−BP,即AD = CP.
∵AQ//BC,
∴四边形APCD是平行四边形,
∴PA//CD,故选项A正确,不符合题意;
B:
∵PA = CD,如图:

四边形APCD可能是等腰梯形,
∴不能推出PA与CD一定平行,故选项B错误,符合题意;
C:
∵∠BAP = ∠DCQ,
∴∠BAQ−∠BAP = ∠BCQ−∠DCQ,
即∠PAQ = ∠BCD.
∵AQ//BC,
∴∠PAQ + ∠APC = ∠BCD + ∠ADC = 180°,
∴∠APC = ∠ADC,
∴∠PAQ + ∠ADC = 180°,
∴PA//CD,故选项C正确,不符合题意;
D:
∵∠APB = ∠CDQ,
∴∠APC = ∠ADC,
同理C选项,得∠PAQ + ∠ADC = 180°,
∴PA//CD,故选项D正确,不符合题意.
10. 核心素养·抽象能力 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC + BC = 4$,以$AB$为边作正方形$ABDE$,连接$CD$,设$BC = x$,四边形$ACDE$的面积为$y$,则$y$关于$x$的函数图象为(
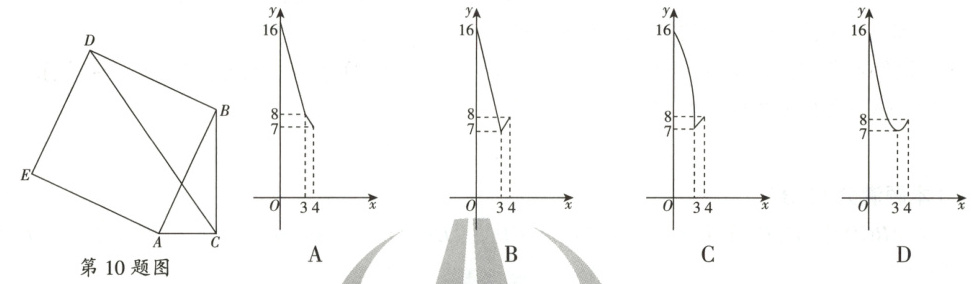
A.图A
B.图B
C.图C
D.图D
D
)
A.图A
B.图B
C.图C
D.图D
答案:
10.D 【解析】如图,连接AD,过点D作DF⊥AC,与CA的延长线交于点F,过点B作BG⊥DF于点G.

∵∠ACB = 90°,
∴四边形BCFG为矩形,
∴∠CBG = 90°,GF = BC,
∴∠ABC + ∠ABG = ∠DBG + ∠ABG = 90°,
∴∠ABC = ∠DBG.
在△ABC和△DBG中,
$\begin{cases} \angle BCA = \angle BGD = 90^{\circ}, \\ \angle ABC = \angle DBG, \\ AB = DB, \end{cases}$
∴△ABC ≌ △DBG(AAS),
∴AC = DG.
∵GF = BC,
∴DF = DG + GF = AC + BC = 4.
设BC = x,则AC = 4 - x,
∴AB² = x² + (4 - x)²,S△ADE = $\frac{1}{2}$AB² = $\frac{1}{2}$x² + $\frac{1}{2}$(4 - x)²,S△ACD = $\frac{1}{2}$AC·DF = $\frac{1}{2}$ × 4(4 - x).
∵y = S△ADE + S△ACD,
∴y = x² - 6x + 16 = (x - 3)² + 7且0 < x < 4,
观察图象可知选项D符合函数关系.
10.D 【解析】如图,连接AD,过点D作DF⊥AC,与CA的延长线交于点F,过点B作BG⊥DF于点G.

∵∠ACB = 90°,
∴四边形BCFG为矩形,
∴∠CBG = 90°,GF = BC,
∴∠ABC + ∠ABG = ∠DBG + ∠ABG = 90°,
∴∠ABC = ∠DBG.
在△ABC和△DBG中,
$\begin{cases} \angle BCA = \angle BGD = 90^{\circ}, \\ \angle ABC = \angle DBG, \\ AB = DB, \end{cases}$
∴△ABC ≌ △DBG(AAS),
∴AC = DG.
∵GF = BC,
∴DF = DG + GF = AC + BC = 4.
设BC = x,则AC = 4 - x,
∴AB² = x² + (4 - x)²,S△ADE = $\frac{1}{2}$AB² = $\frac{1}{2}$x² + $\frac{1}{2}$(4 - x)²,S△ACD = $\frac{1}{2}$AC·DF = $\frac{1}{2}$ × 4(4 - x).
∵y = S△ADE + S△ACD,
∴y = x² - 6x + 16 = (x - 3)² + 7且0 < x < 4,
观察图象可知选项D符合函数关系.
11. 若分式$\dfrac{5}{x + 2}$有意义,则$x$的取值范围是$$_________$$。
答案:
11.x≠−2
12. 为了比较$\sqrt{29}$与$\sqrt{13} + 2$的大小,我们可以构造如图所示的图形进行推算,其中$\angle C = 90^{\circ}$,$BC = 5$,点$D$在$BC$上且$CD = 3$,$AC = 2$。通过计算可得$\sqrt{29}$ _________ $\sqrt{13} + 2$。(选填“$>$”“$<$”或“$=$”)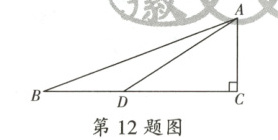

答案:
12.<
13. 跨学科·物理 从“熔化”“燃烧”“遗传”“升华”4种现象中同时任选2种,都属于物理现象的概率是$$
$\frac{1}{6}$
$$。
答案:
13.$\frac{1}{6}$
14. 如图,$\triangle ABC$的2个内角$\angle ABC$与$\angle ACB$的平分线相交于点$I$。
(1)设$\angle A = \alpha$,则$\angle BIC = $
(2)过点$I$的直线分别交$AB$,$AC$于$D$,$E$两点,$\triangle ADE$,$\triangle ABC$的面积分别记为$S_{\triangle ADE}$,$S_{\triangle ABC}$。若$\dfrac{S_{\triangle ADE}}{S_{\triangle ABC}} = \dfrac{2}{5}$,$\triangle ABC$的周长为8,则$AD + AE$的值为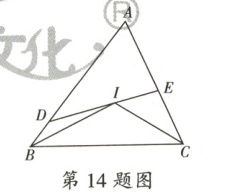
(1)设$\angle A = \alpha$,则$\angle BIC = $
90°+$\frac{1}{2}α$
。(用含$\alpha$的式子表示)(2)过点$I$的直线分别交$AB$,$AC$于$D$,$E$两点,$\triangle ADE$,$\triangle ABC$的面积分别记为$S_{\triangle ADE}$,$S_{\triangle ABC}$。若$\dfrac{S_{\triangle ADE}}{S_{\triangle ABC}} = \dfrac{2}{5}$,$\triangle ABC$的周长为8,则$AD + AE$的值为
$\frac{16}{5}$
。
答案:
14.
(1)90°+$\frac{1}{2}$α
(2)$\frac{16}{5}$ 【解析】
(1)由条件可知∠ABC + ∠ACB = 180° - α.
∵∠ABC与∠ACB的平分线相交于点I,
∴∠IBC = $\frac{1}{2}$∠ABC,∠ICB = $\frac{1}{2}$∠ACB,
∴∠BIC = 180° - ∠IBC - ∠ICB
= 180° - $\frac{1}{2}$∠ABC - $\frac{1}{2}$∠ACB
= 180° - $\frac{1}{2}$(180° - α)
= 90° + $\frac{1}{2}$α.
故答案为90° + $\frac{1}{2}$α.
(2)如图,连接AI,作IF⊥AB于点F,IG⊥BC于点G,IH⊥AC于点H.
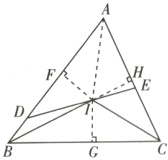
由条件可知IF = IG = IH,
∴S△ABC = S△AIB + S△AIC + S△BIC = $\frac{1}{2}$IG(AB + BC + AC),
S△ADE = $\frac{1}{2}$(AD·IF + AE·IH) = $\frac{1}{2}$IG(AD + AE).
∵$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}$ = $\frac{2}{5}$,
∴$\frac{AD + AE}{AB + AC + BC}$ = $\frac{2}{5}$.
又
∵AB + AC + BC = 8,
∴AD + AE = $\frac{16}{5}$.
故答案为$\frac{16}{5}$.
14.
(1)90°+$\frac{1}{2}$α
(2)$\frac{16}{5}$ 【解析】
(1)由条件可知∠ABC + ∠ACB = 180° - α.
∵∠ABC与∠ACB的平分线相交于点I,
∴∠IBC = $\frac{1}{2}$∠ABC,∠ICB = $\frac{1}{2}$∠ACB,
∴∠BIC = 180° - ∠IBC - ∠ICB
= 180° - $\frac{1}{2}$∠ABC - $\frac{1}{2}$∠ACB
= 180° - $\frac{1}{2}$(180° - α)
= 90° + $\frac{1}{2}$α.
故答案为90° + $\frac{1}{2}$α.
(2)如图,连接AI,作IF⊥AB于点F,IG⊥BC于点G,IH⊥AC于点H.

由条件可知IF = IG = IH,
∴S△ABC = S△AIB + S△AIC + S△BIC = $\frac{1}{2}$IG(AB + BC + AC),
S△ADE = $\frac{1}{2}$(AD·IF + AE·IH) = $\frac{1}{2}$IG(AD + AE).
∵$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}$ = $\frac{2}{5}$,
∴$\frac{AD + AE}{AB + AC + BC}$ = $\frac{2}{5}$.
又
∵AB + AC + BC = 8,
∴AD + AE = $\frac{16}{5}$.
故答案为$\frac{16}{5}$.
15. 核心素养·运算能力 解不等式:$\dfrac{x}{2} - 1 < x$。
答案:
15.解:$\frac{x}{2}$ - 1 < x,
x - 2 < 2x,(4分)
-x < 2,(6分)
x > -2.(8分)
x - 2 < 2x,(4分)
-x < 2,(6分)
x > -2.(8分)
查看更多完整答案,请扫码查看


