第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
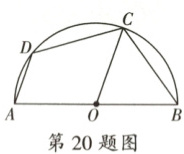
20. 如图,四边形$ ABCD $的顶点都在半圆$ O $上,$ AB $是半圆$ O $的直径,连接$ OC $,$ \angle DAB + 2\angle ABC = 180° $.
(1) 求证:$ OC // AD $.
(2) 若$ AD = 2 $,$ BC = 2\sqrt{3} $,求$ AB $的长.
(1) 求证:$ OC // AD $.
(2) 若$ AD = 2 $,$ BC = 2\sqrt{3} $,求$ AB $的长.

答案:
20.解:
(1)证明:$\because \angle AOC = 2\angle ABC$,$\angle DAB + 2\angle ABC = 180°$,$\therefore \angle DAB + \angle AOC = 180°$,$\therefore OC // AD$。(5分)
(2)如图,连接$BD$,交$OC$于点$E$。

$\because AB$是$\odot O$的直径,$\therefore \angle ADB = 90°$,即$AD \perp BD$。
$\because OC // AD$,$\therefore OC \perp BD$,$\therefore$点$E$为$BD$的中点。
又$\because$点$O$是$AB$的中点,$\therefore OE$是$\triangle ABD$的中位线,$\therefore OE = \frac{1}{2}AD = 1$。
设半圆的半径为$r$,则$CE = r - 1$。
由勾股定理知,$OB^2 - OE^2 = BE^2 = BC^2 - CE^2$,即$r^2 - 1 = (2\sqrt{3})^2 - (r - 1)^2$,
解得$r_1 = 3$,$r_2 = -2$(舍去),$\therefore AB = 2r = 6$。(10分)
20.解:
(1)证明:$\because \angle AOC = 2\angle ABC$,$\angle DAB + 2\angle ABC = 180°$,$\therefore \angle DAB + \angle AOC = 180°$,$\therefore OC // AD$。(5分)
(2)如图,连接$BD$,交$OC$于点$E$。

$\because AB$是$\odot O$的直径,$\therefore \angle ADB = 90°$,即$AD \perp BD$。
$\because OC // AD$,$\therefore OC \perp BD$,$\therefore$点$E$为$BD$的中点。
又$\because$点$O$是$AB$的中点,$\therefore OE$是$\triangle ABD$的中位线,$\therefore OE = \frac{1}{2}AD = 1$。
设半圆的半径为$r$,则$CE = r - 1$。
由勾股定理知,$OB^2 - OE^2 = BE^2 = BC^2 - CE^2$,即$r^2 - 1 = (2\sqrt{3})^2 - (r - 1)^2$,
解得$r_1 = 3$,$r_2 = -2$(舍去),$\therefore AB = 2r = 6$。(10分)
21. 新情境 综合与实践
【项目主题】
某劳动实践小组拟用正三角形和正六边形两种环保组件改善小区幼儿园室内活动场地.
【项目准备】
(1) 密铺知识学习:用形状、大小完全相同的一种或几种平面图形进行拼接,使图形之间既没有空隙也没有重叠地铺成一片,叫作图形的密铺.
(2) 密铺方式构建:运用密铺知识得到如图1、图2所示的两种拼接方式,其中正六边形和正三角形组件的边长均为20 cm.
(3) 密铺规律探究:为方便研究,称图3、图4分别为图1、图2的拼接单元.
观察发现:自左向右拼接图1时,每增加一个如图3所示的拼接单元,则增加1个正六边形和2个正三角形,长度增加40 cm,从而$ x $个这样的拼接单元拼成一行的长度为$ (40x + 10) \, cm $.
自左向右拼接图2时,每增加一个如图4所示的拼接单元,则增加 ① 个正六边形和 ② 个正三角形,长度增加 ③ cm,从而$ y $个这样的拼接单元拼成一行的长度为 ④ cm.
【项目分析】
(1) 项目条件:场地为长7.4 m、宽6 m的矩形;正三角形和正六边形组件的单价分别为1元和5元.
(2) 基本约定:项目成本仅计算所需组件的费用.
(3) 方式确定:
(i) 考虑成本因素,采用图1方式进行密铺;
(ii) 每行用正六边形组件顶着左墙开始,从左向右用一个正六边形与两个正三角形组件按图1所示方式依次交替拼接,当不能继续拼接时,该行拼接结束;
(iii) 第一行紧靠墙边,从前往后按相同方式逐行密铺,直至不能拼接为止.
(4) 方案论证:按上述确定的方式进行密铺,有以下两种方案.
方案一:第一行沿着长度为6 m的墙自左向右拼接(如图5).
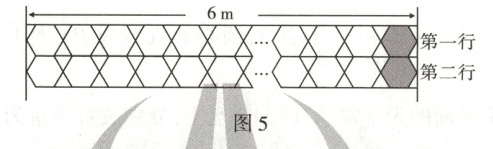
根据规律,令$ 40x + 10 \leq 600 $,解得$ x \leq 14.75 $,所以每行可以先拼14块拼接单元,即共用去14个正六边形和28个正三角形组件,由$ 40 × 14 + 10 = 570 $知,所拼长度为570 cm,剩余30 cm恰好还可以摆放一个正六边形组件(如图5所示的阴影正六边形).最终需用15个正六边形和28个正三角形组件,由$ 5 × 15 + 1 × 28 = 103 $知,方案一每行的成本为103元.
由于每行宽度为$ 20\sqrt{3} \, cm $(按$ \sqrt{3} = 1.73 $计算),设拼成$ s $行,则$ 20\sqrt{3}s \leq 740 $,解得$ s \leq \frac{37\sqrt{3}}{3} \approx 21.34 $,故需铺21行.由$ 103 × 21 = 2163 $知,方案一所需的总成本为2163元.
方案二:第一行沿着长度为7.4 m的墙自左向右拼接.
类似于方案一的成本计算,令$ 40x + 10 \leq 740 $……
方案二每行的成本为 ⑤ 元,总成本为 ⑥ 元.
【项目实施】
根据以上分析,选用总成本较少的方案完成实践活动(略).
请将上述材料中横线上所缺内容补充完整:
① $ $
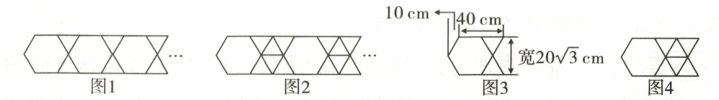
【项目主题】
某劳动实践小组拟用正三角形和正六边形两种环保组件改善小区幼儿园室内活动场地.
【项目准备】
(1) 密铺知识学习:用形状、大小完全相同的一种或几种平面图形进行拼接,使图形之间既没有空隙也没有重叠地铺成一片,叫作图形的密铺.
(2) 密铺方式构建:运用密铺知识得到如图1、图2所示的两种拼接方式,其中正六边形和正三角形组件的边长均为20 cm.
(3) 密铺规律探究:为方便研究,称图3、图4分别为图1、图2的拼接单元.
观察发现:自左向右拼接图1时,每增加一个如图3所示的拼接单元,则增加1个正六边形和2个正三角形,长度增加40 cm,从而$ x $个这样的拼接单元拼成一行的长度为$ (40x + 10) \, cm $.
自左向右拼接图2时,每增加一个如图4所示的拼接单元,则增加 ① 个正六边形和 ② 个正三角形,长度增加 ③ cm,从而$ y $个这样的拼接单元拼成一行的长度为 ④ cm.
【项目分析】
(1) 项目条件:场地为长7.4 m、宽6 m的矩形;正三角形和正六边形组件的单价分别为1元和5元.
(2) 基本约定:项目成本仅计算所需组件的费用.
(3) 方式确定:
(i) 考虑成本因素,采用图1方式进行密铺;
(ii) 每行用正六边形组件顶着左墙开始,从左向右用一个正六边形与两个正三角形组件按图1所示方式依次交替拼接,当不能继续拼接时,该行拼接结束;
(iii) 第一行紧靠墙边,从前往后按相同方式逐行密铺,直至不能拼接为止.
(4) 方案论证:按上述确定的方式进行密铺,有以下两种方案.
方案一:第一行沿着长度为6 m的墙自左向右拼接(如图5).

根据规律,令$ 40x + 10 \leq 600 $,解得$ x \leq 14.75 $,所以每行可以先拼14块拼接单元,即共用去14个正六边形和28个正三角形组件,由$ 40 × 14 + 10 = 570 $知,所拼长度为570 cm,剩余30 cm恰好还可以摆放一个正六边形组件(如图5所示的阴影正六边形).最终需用15个正六边形和28个正三角形组件,由$ 5 × 15 + 1 × 28 = 103 $知,方案一每行的成本为103元.
由于每行宽度为$ 20\sqrt{3} \, cm $(按$ \sqrt{3} = 1.73 $计算),设拼成$ s $行,则$ 20\sqrt{3}s \leq 740 $,解得$ s \leq \frac{37\sqrt{3}}{3} \approx 21.34 $,故需铺21行.由$ 103 × 21 = 2163 $知,方案一所需的总成本为2163元.
方案二:第一行沿着长度为7.4 m的墙自左向右拼接.
类似于方案一的成本计算,令$ 40x + 10 \leq 740 $……
方案二每行的成本为 ⑤ 元,总成本为 ⑥ 元.
【项目实施】
根据以上分析,选用总成本较少的方案完成实践活动(略).
请将上述材料中横线上所缺内容补充完整:
① $ $
1
$ $;② $ $6
$ $;③ $ $60
$ $;④ $ $60y+10
$ $;⑤ $ $126
$ $;⑥ $ $2142
$ $.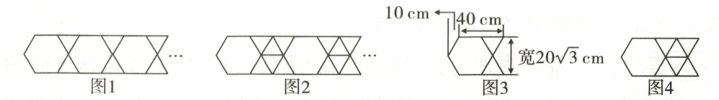
答案:
21.解:①$1$;(2分)②$6$;(4分)③$60$;(6分)④$60y + 10$;(8分)⑤$126$;(10分)⑥$2142$。(12分)
查看更多完整答案,请扫码查看


