第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
18. 数学兴趣小组在计算$15× 15$,$25× 25$,$36× 34$等两位数乘法时发现,当十位上的数字相同、个位上的数字之和为10的两个两位数相乘时可以用图形面积来分解计算:
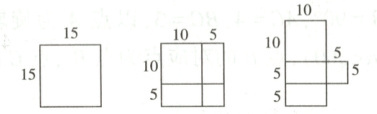
由上图可得$15× 15 = 10× 20 + 5× 5 = 225$;

由上图可得$25× 25 = 20× 30 + 5× 5 = 625$;
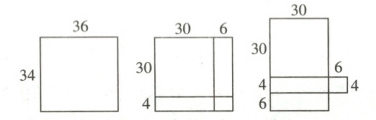
由上图可得$36× 34 = 30× 40 + 6× 4 = 1224$。
(1)请你帮助数学兴趣小组画出计算$62× 68$的面积分解图并计算。
(2)设这两个两位数的十位数字为$a$,个位数字分别为$b$,$c$,请用含$a$,$b$,$c$的代数式表示出你发现的计算规律,并证明。

由上图可得$15× 15 = 10× 20 + 5× 5 = 225$;

由上图可得$25× 25 = 20× 30 + 5× 5 = 625$;

由上图可得$36× 34 = 30× 40 + 6× 4 = 1224$。
(1)请你帮助数学兴趣小组画出计算$62× 68$的面积分解图并计算。
(2)设这两个两位数的十位数字为$a$,个位数字分别为$b$,$c$,请用含$a$,$b$,$c$的代数式表示出你发现的计算规律,并证明。
答案:
18.解:
(1)如图,

由图可得$62 × 68 = 60 × 70 + 2 × 8 = 4216$.(4分)
(2)$(10a + b)(10a + c) = 10a · 10(a + 1) + bc$.
证明:根据多项式乘多项式的运算法则可得:
左边$= 100a^2 + 10a(b + c) + bc$,
右边$= 10a · 10(a + 1) + bc = 100a^2 + 100a + bc$,
$\therefore$该等式成立.(8分)
18.解:
(1)如图,

由图可得$62 × 68 = 60 × 70 + 2 × 8 = 4216$.(4分)
(2)$(10a + b)(10a + c) = 10a · 10(a + 1) + bc$.
证明:根据多项式乘多项式的运算法则可得:
左边$= 100a^2 + 10a(b + c) + bc$,
右边$= 10a · 10(a + 1) + bc = 100a^2 + 100a + bc$,
$\therefore$该等式成立.(8分)
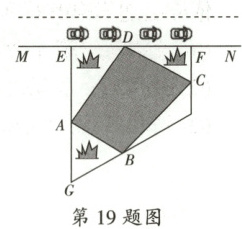
19. 如图,市区内某公路$MN$旁有一个四边形池塘(四边形$ABCD$),池塘外围是三个小公园,涛涛同学为了了解池塘的最大跨度(即$AC$的长度),他和同学们利用皮尺和测角仪进行了测量,得到如下数据:$AE\perp MN$,$CF\perp MN$,$AE = 147\mathrm{m}$,$CF = 77\mathrm{m}$,$\angle ADE = 55.8^{\circ}$,$\angle CDF = 28.9^{\circ}$,请你根据以上信息,帮助涛涛同学计算出该池塘的最大跨度。(参考数据:$\sin 55.8^{\circ}\approx 0.83$,$\cos 55.8^{\circ}\approx 0.56$,$\tan 55.8^{\circ}\approx 1.47$,$\sin 28.9^{\circ}\approx 0.48$,$\cos 28.9^{\circ}\approx 0.88$,$\tan 28.9^{\circ}\approx 0.55$)

答案:
19.解:过点$C$作$CH \perp AE$于点$H$,连接$AC$.

在$Rt\triangle AED$中,$AE = 147 m$,$\angle ADE = 55.8°$,
$\tan \angle ADE = \frac{AE}{ED}$,
$\therefore ED = \frac{AE}{\tan \angle ADE} \approx \frac{147}{1.47} = 100(m)$.(3分)
在$Rt\triangle DFC$中,$CF = 77 m$,$\angle CDF = 28.9°$,
$\tan \angle CDF = \frac{CF}{DF}$,
$\therefore DF = \frac{CF}{\tan \angle CDF} \approx \frac{77}{0.55} = 140(m)$.(6分)
$\because AE \perp MN$,$CF \perp MN$,$CH \perp AE$,
$\therefore HC = EF = ED + DF = 240 m$,
$AH = AE - EH = AE - CF = 70 m$.
根据勾股定理,得$AC = \sqrt{AH^2 + HC^2} = 250 m$.
答:该池塘的最大跨度约为$250 m$.(10分)
19.解:过点$C$作$CH \perp AE$于点$H$,连接$AC$.

在$Rt\triangle AED$中,$AE = 147 m$,$\angle ADE = 55.8°$,
$\tan \angle ADE = \frac{AE}{ED}$,
$\therefore ED = \frac{AE}{\tan \angle ADE} \approx \frac{147}{1.47} = 100(m)$.(3分)
在$Rt\triangle DFC$中,$CF = 77 m$,$\angle CDF = 28.9°$,
$\tan \angle CDF = \frac{CF}{DF}$,
$\therefore DF = \frac{CF}{\tan \angle CDF} \approx \frac{77}{0.55} = 140(m)$.(6分)
$\because AE \perp MN$,$CF \perp MN$,$CH \perp AE$,
$\therefore HC = EF = ED + DF = 240 m$,
$AH = AE - EH = AE - CF = 70 m$.
根据勾股定理,得$AC = \sqrt{AH^2 + HC^2} = 250 m$.
答:该池塘的最大跨度约为$250 m$.(10分)
查看更多完整答案,请扫码查看


