《2026年秒杀中考数学安徽专版》

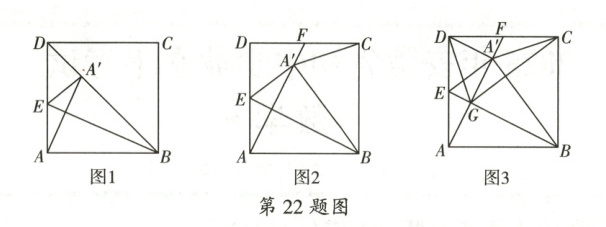
22. 核心素养·几何直观 已知点$ A' $在正方形$ ABCD $内,点$ E $在边$ AD $上,$ BE $是线段$ AA' $的垂直平分线,连接$ A'E $,$ A'B $.
(1) 如图1,若$ BA' $的延长线经过点$ D $,$ AE = 1 $,求$ AB $的长.
(2) 如图2,点$ F $是$ AA' $的延长线与$ CD $的交点,连接$ CA' $.
(i) 求证:$ \angle CA'F = 45° $;
(ii) 如图3,设$ AF,BE $相交于点$ G $,连接$ CG,DG,DA' $.若$ CG = CB $,判断$ \triangle A'DG $的形状,并说明理由.
 

答案：
22.解：
(1)$\because$四边形$ABCD$是正方形，$BA'$的延长线经过点$D$，$\therefore \angle ADB = 45°$，$AD = AB$，$\angle DAB = 90°$。由垂直平分线的性质知，$A'E = AE$，$BA' = BA$。又$BE = BE$，$\therefore \triangle EA'B \cong \triangle EAB(SSS)$，$\therefore \angle EA'B = \angle EAB = 90°$。又$\angle ADB = 45°$，$\therefore \triangle A'DE$是等腰直角三角形，$\therefore A'E = AE = 1$，$\therefore DE = \sqrt{2}A'E = \sqrt{2}$，$\therefore AB = AD = AE + DE = 1 + \sqrt{2}$。(4分)
(2)(i)证明：由题意知，$BA = BA' = BC$，$\therefore \angle BAA' = \angle BA'A$，$\angle BCA' = \angle BA'C$，$\therefore \angle AA'C = \angle AA'B + \angle CA'B$
$=\frac{1}{2}(180° - \angle ABA') + \frac{1}{2}(180° - \angle CBA')$
$= 180° - \frac{1}{2}(\angle ABA' + \angle CBA')$
$= 180° - \frac{1}{2} × 90°$
$= 135°$，
$\therefore \angle CA'F = 180° - \angle AA'C = 45°$。(8分)
(ii)$\triangle A'DG$是等腰直角三角形。理由如下：
如图，作$CN \perp BG$交$BG$于点$M$，交$AB$于点$N$。

$\because CG = CB$，$\therefore$点$M$为$BG$的中点。
又$AA' \perp BE$，$\therefore CN // AF$，$\therefore \frac{BN}{AN} = \frac{BM}{GM} = 1$，$\therefore$点$N$是$AB$的中点，$\therefore MN$是$\triangle ABG$的中位线，$BN = \frac{1}{2}AB$。(10分)
$\because \angle ABE = 90° - \angle CBG = \angle BCN$，$\angle BAE = \angle CBN = 90°$，且$AB = BC$，$\therefore \triangle ABE \cong \triangle BCN(ASA)$，$\therefore AE = BN = \frac{1}{2}AB = \frac{1}{2}AD$，即点$E$为$AD$的中点。
又$AG = GA'$，$\therefore EG // A'D$，$\therefore \angle DA'G = \angle EGA = 90°$。
同理可证$\triangle ADA' \cong \triangle BAG$，$\therefore A'D = AG = A'G$，$\therefore \triangle A'DG$是等腰直角三角形。(12分)