第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
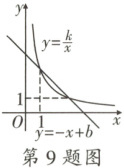
9. 已知反比例函数$y = \frac{k}{x}(k \neq 0)$在第一象限内的图象与一次函数$y = -x + b$的图象如图所示,则函数$y = x^2 - bx + k - 1$的图象可能为(
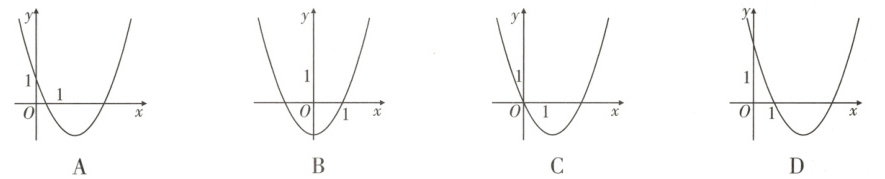
.
A
)
.

答案:
9.A [解析]本题考查一次函数与反比例函数的交点问题、二次函数的图象识别.

如图,设点A的坐标为$(1,k)$,则点B的坐标为$(k,1)$,且$k > 1$.
将点$B(k,1)$代入$y = -x + b$,得$1 = -k + b$,
则$k = b - 1 > 1$,$\therefore b > 2$.
$\because y = x^{2} - bx + k - 1 = x^{2} - bx + b - 2 = (x - \frac{b}{2})^{2} + \frac{b^{2}}{4} + b - 2$,
$\therefore$函数$y = x^{2} - bx + k - 1$的图象的对称轴为直线$x = \frac{b}{2} > 1$,在直线$x = 1$的右侧.
$\because$当$x = 1$时,$y = 1 - b + b - 2 = -1$,
当$x = 0$时,$y = b - 2 > 0$,
$\therefore$函数$y = x^{2} - bx + k - 1$的图象经过点$(1, -1)$,与$y$轴的交点在$x$轴上方.
综上所述,在四个图象中,只有A选项符合.
9.A [解析]本题考查一次函数与反比例函数的交点问题、二次函数的图象识别.

如图,设点A的坐标为$(1,k)$,则点B的坐标为$(k,1)$,且$k > 1$.
将点$B(k,1)$代入$y = -x + b$,得$1 = -k + b$,
则$k = b - 1 > 1$,$\therefore b > 2$.
$\because y = x^{2} - bx + k - 1 = x^{2} - bx + b - 2 = (x - \frac{b}{2})^{2} + \frac{b^{2}}{4} + b - 2$,
$\therefore$函数$y = x^{2} - bx + k - 1$的图象的对称轴为直线$x = \frac{b}{2} > 1$,在直线$x = 1$的右侧.
$\because$当$x = 1$时,$y = 1 - b + b - 2 = -1$,
当$x = 0$时,$y = b - 2 > 0$,
$\therefore$函数$y = x^{2} - bx + k - 1$的图象经过点$(1, -1)$,与$y$轴的交点在$x$轴上方.
综上所述,在四个图象中,只有A选项符合.
10. 如图,$E$是线段$AB$上一点,$\triangle ADE$和$\triangle BCE$是位于直线$AB$同侧的两个等边三角形,点$P$,$F$分别是$CD$,$AB$的中点。若$AB = 4$,则下列结论中错误的是(
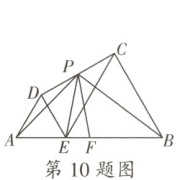
A.$PA + PB$的最小值为$3\sqrt{3}$
B.$PE + PF$
C.$\triangle CDE$周长的最小值为$6$
D.四边形$ABCD$面积的最小值为$3\sqrt{3}$
A
)
A.$PA + PB$的最小值为$3\sqrt{3}$
B.$PE + PF$
的
最小值为$2\sqrt{3}$C.$\triangle CDE$周长的最小值为$6$
D.四边形$ABCD$面积的最小值为$3\sqrt{3}$
答案:
10.A [解析]本题考查几何图形的最值问题,涉及轴对称求最值、三点共线最值、利用二次函数求最值,综合性很强,求出点P的运动路径是解题的关键.

$\because \triangle ADE$和$\triangle BCE$是等边三角形,
$\therefore \angle DEA = \angle QBA = 60^{\circ}$,$\angle CEB = \angle QAB = 60^{\circ}$,
$\therefore DE // BQ$,$CE // AQ$,
$\therefore$四边形DECQ是平行四边形.
$\because$点P为线段CD的中点,$\therefore EP = \frac{1}{2}EQ$.
$\because$点E在线段AB上运动,
$\therefore$点P在线段MN上运动.
由$AB = 4$,知等边三角形ABQ的高为$2\sqrt{3}$,则点P到直线AB的距离为$\sqrt{3}$.
作A关于直线MN的对称点$A'$,连接$A'B$,当点P运动到$A'$,$P$,$B$共线时,$PA + PB = PA' + PB$最小,此时$PA + PB$最小值为$A'B = \sqrt{AA'^{2} + AB^{2}} = \sqrt{(2\sqrt{3})^{2} + 4^{2}} = 2\sqrt{7}$,故选项A错误,符合题意;
$\because PQ = PE$,$\therefore PE + PF = PQ + PF$,
$\therefore$当$Q$,$P$,$F$三点共线时,$PE + PF$最小,最小值为QF的长度.
$\because F$为AB的中点,$\therefore QF \perp AB$,
$\therefore QF$为等边三角形ABQ的高,
$\therefore PE + PF$的最小值为$2\sqrt{3}$,故选项B正确,不符合题意;
如图,过点D作$DK \perp AB$于点K,过点C作$CT \perp AB$于点T,

$\because \triangle ADE$和$\triangle BCE$都是等边三角形,
$\therefore KE = \frac{1}{2}AE$,$TE = \frac{1}{2}BE$,
$\therefore KT = KE + TE = \frac{1}{2}AB = 2$,
$\therefore CD \geq 2$,
$\therefore DE + CE + CD = AE + BE + CD = AB + CD \geq 6$,
$\therefore \triangle CDE$周长的最小值为6,故选项C正确,不符合题意;
设$AE = 2m$,则$BE = 4 - 2m$,
$\therefore AK = KE = m$,$BT = ET = 2 - m$,
$DK = \sqrt{3}AK = \sqrt{3}m$,$CT = \sqrt{3}BT = 2\sqrt{3} - \sqrt{3}m$,
$\therefore S_{\triangle ADK} = \frac{1}{2} · m · \sqrt{3}m = \frac{\sqrt{3}}{2}m^{2}$,$S_{\triangle BCT} = \frac{1}{2}(2 - m) · (2\sqrt{3} - \sqrt{3}m) = \frac{\sqrt{3}}{2}m^{2} - 2\sqrt{3}m + 2\sqrt{3}$,
$S_{梯形DKTC} = \frac{1}{2}(\sqrt{3}m + 2\sqrt{3} - \sqrt{3}m) · 2 = 2\sqrt{3}$,
$\therefore S_{四边形ABCD} = \frac{\sqrt{3}}{2}m^{2} + \frac{\sqrt{3}}{2}m^{2} - 2\sqrt{3}m + 2\sqrt{3} + 2\sqrt{3} = \sqrt{3}m^{2} - 2\sqrt{3}m + 4\sqrt{3} = \sqrt{3}(m - 1)^{2} + 3\sqrt{3}$,
$\therefore$当$m = 1$时,四边形ABCD面积的最小值为$3\sqrt{3}$,故选项D正确,不符合题意.
10.A [解析]本题考查几何图形的最值问题,涉及轴对称求最值、三点共线最值、利用二次函数求最值,综合性很强,求出点P的运动路径是解题的关键.

$\because \triangle ADE$和$\triangle BCE$是等边三角形,
$\therefore \angle DEA = \angle QBA = 60^{\circ}$,$\angle CEB = \angle QAB = 60^{\circ}$,
$\therefore DE // BQ$,$CE // AQ$,
$\therefore$四边形DECQ是平行四边形.
$\because$点P为线段CD的中点,$\therefore EP = \frac{1}{2}EQ$.
$\because$点E在线段AB上运动,
$\therefore$点P在线段MN上运动.
由$AB = 4$,知等边三角形ABQ的高为$2\sqrt{3}$,则点P到直线AB的距离为$\sqrt{3}$.
作A关于直线MN的对称点$A'$,连接$A'B$,当点P运动到$A'$,$P$,$B$共线时,$PA + PB = PA' + PB$最小,此时$PA + PB$最小值为$A'B = \sqrt{AA'^{2} + AB^{2}} = \sqrt{(2\sqrt{3})^{2} + 4^{2}} = 2\sqrt{7}$,故选项A错误,符合题意;
$\because PQ = PE$,$\therefore PE + PF = PQ + PF$,
$\therefore$当$Q$,$P$,$F$三点共线时,$PE + PF$最小,最小值为QF的长度.
$\because F$为AB的中点,$\therefore QF \perp AB$,
$\therefore QF$为等边三角形ABQ的高,
$\therefore PE + PF$的最小值为$2\sqrt{3}$,故选项B正确,不符合题意;
如图,过点D作$DK \perp AB$于点K,过点C作$CT \perp AB$于点T,

$\because \triangle ADE$和$\triangle BCE$都是等边三角形,
$\therefore KE = \frac{1}{2}AE$,$TE = \frac{1}{2}BE$,
$\therefore KT = KE + TE = \frac{1}{2}AB = 2$,
$\therefore CD \geq 2$,
$\therefore DE + CE + CD = AE + BE + CD = AB + CD \geq 6$,
$\therefore \triangle CDE$周长的最小值为6,故选项C正确,不符合题意;
设$AE = 2m$,则$BE = 4 - 2m$,
$\therefore AK = KE = m$,$BT = ET = 2 - m$,
$DK = \sqrt{3}AK = \sqrt{3}m$,$CT = \sqrt{3}BT = 2\sqrt{3} - \sqrt{3}m$,
$\therefore S_{\triangle ADK} = \frac{1}{2} · m · \sqrt{3}m = \frac{\sqrt{3}}{2}m^{2}$,$S_{\triangle BCT} = \frac{1}{2}(2 - m) · (2\sqrt{3} - \sqrt{3}m) = \frac{\sqrt{3}}{2}m^{2} - 2\sqrt{3}m + 2\sqrt{3}$,
$S_{梯形DKTC} = \frac{1}{2}(\sqrt{3}m + 2\sqrt{3} - \sqrt{3}m) · 2 = 2\sqrt{3}$,
$\therefore S_{四边形ABCD} = \frac{\sqrt{3}}{2}m^{2} + \frac{\sqrt{3}}{2}m^{2} - 2\sqrt{3}m + 2\sqrt{3} + 2\sqrt{3} = \sqrt{3}m^{2} - 2\sqrt{3}m + 4\sqrt{3} = \sqrt{3}(m - 1)^{2} + 3\sqrt{3}$,
$\therefore$当$m = 1$时,四边形ABCD面积的最小值为$3\sqrt{3}$,故选项D正确,不符合题意.
11. 计算:$\sqrt[3]{8} + 1 = $
3
$$。
答案:
11.3 [解析]本题考查求一个数的立方根.
$\sqrt[3]{8} + 1 = 2 + 1 = 3$.
$\sqrt[3]{8} + 1 = 2 + 1 = 3$.
12. 据统计,2023年第一季度安徽省采矿业实现利润总额74.5亿元,其中74.5亿用科学记数法表示为$$
7.45×10⁹
$$。
答案:
12.$7.45 × 10^{9}$ [解析]本题考查科学记数法.
74.5亿$= 74.5 × 10^{8} = 7.45 × 10^{9}$.
74.5亿$= 74.5 × 10^{8} = 7.45 × 10^{9}$.
13. 数学文化 清初数学家梅文鼎在著作《平三角举要》中,对南宋数学家秦九韶提出的计算三角形面积的“三斜求积术”给出了一个完整的证明,证明过程中创造性地设计直角三角形,得出了一个结论:如图,$AD$是锐角$\triangle ABC$的高,则$BD = \frac{1}{2}\left(BC + \frac{AB^2 - AC^2}{BC}\right)$。当$AB = 7$,$BC = 6$,$AC = 5$时,$CD = $
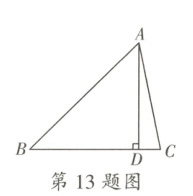
1
$$。
答案:
13.1 [解析]本题考查三角形的高的定义.
$\because AB = 7$,$BC = 6$,$AC = 5$,
$\therefore BD = \frac{1}{2}(\frac{AB^{2} - AC^{2}}{BC} + BC) = \frac{1}{2}(\frac{49 - 25}{6} + 6) = 5$,
$\therefore CD = BC - BD = 1$.
$\because AB = 7$,$BC = 6$,$AC = 5$,
$\therefore BD = \frac{1}{2}(\frac{AB^{2} - AC^{2}}{BC} + BC) = \frac{1}{2}(\frac{49 - 25}{6} + 6) = 5$,
$\therefore CD = BC - BD = 1$.
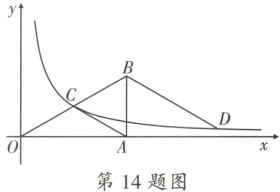
14. 如图,$O$是坐标原点,$Rt\triangle OAB$的直角顶点$A$在$x$轴的正半轴上,$AB = 2$,$\angle AOB = 30°$,反比例函数$y = \frac{k}{x}(k \gt 0)$的图象经过斜边$OB$的中点$C$。
(1)$k = $
(2)$D$为该反比例函数图象上的一点,若$DB // AC$,则$OB^2 - BD^2$的值为$$
(1)$k = $
√3
$$。(2)$D$为该反比例函数图象上的一点,若$DB // AC$,则$OB^2 - BD^2$的值为$$
4
$$。
答案:
14.
(1)$\sqrt{3}$
(2)4 [解析]本题考查反比例函数与几何图形、勾股定理等知识.
(1)$\because AB = 2$,$\angle AOB = 30^{\circ}$,$\angle OAB = 90^{\circ}$,
$\therefore OA = 2\sqrt{3}$,$OB = 2AB = 4$,
$\therefore A(2\sqrt{3},0)$,$B(2\sqrt{3},2)$.
$\because$点C是OB的中点,
$\therefore$易得点C的坐标为$(\sqrt{3},1)$.
$\because$反比例函数$y = \frac{k}{x}(k > 0)$的图象经过点C,
$\therefore$将$C(\sqrt{3},1)$代入$y = \frac{k}{x}$,得$k = \sqrt{3}$.
(2)$\because \angle AOB = 30^{\circ}$,$\angle OAB = 90^{\circ}$,
$\therefore \angle OBA = 60^{\circ}$.
$\because$点C是边OB的中点,$\therefore AC = BC$,
$\therefore \angle CAB = 60^{\circ}$.
$\because DB // AC$,$\therefore \angle DBA = 60^{\circ}$.
如图,过点D作$DE \perp AB$,垂足为点E.
设$BE = m(m > 0)$,则$DE = \sqrt{3}m$,$BD = 2m$,点D的坐标为$(2\sqrt{3} + \sqrt{3}m,2 - m)$.

$\because$点D为反比例函数$y = \frac{\sqrt{3}}{x}$图象上的一点,
$\therefore (2\sqrt{3} + \sqrt{3}m)(2 - m) = \sqrt{3}$,解得$m = \sqrt{3}$(负值舍去),
$\therefore BD = 2m = 2\sqrt{3}$,
$\therefore OB^{2} - BD^{2} = (2\sqrt{3})^{2} + 2^{2} - (2\sqrt{3})^{2} = 4$.
14.
(1)$\sqrt{3}$
(2)4 [解析]本题考查反比例函数与几何图形、勾股定理等知识.
(1)$\because AB = 2$,$\angle AOB = 30^{\circ}$,$\angle OAB = 90^{\circ}$,
$\therefore OA = 2\sqrt{3}$,$OB = 2AB = 4$,
$\therefore A(2\sqrt{3},0)$,$B(2\sqrt{3},2)$.
$\because$点C是OB的中点,
$\therefore$易得点C的坐标为$(\sqrt{3},1)$.
$\because$反比例函数$y = \frac{k}{x}(k > 0)$的图象经过点C,
$\therefore$将$C(\sqrt{3},1)$代入$y = \frac{k}{x}$,得$k = \sqrt{3}$.
(2)$\because \angle AOB = 30^{\circ}$,$\angle OAB = 90^{\circ}$,
$\therefore \angle OBA = 60^{\circ}$.
$\because$点C是边OB的中点,$\therefore AC = BC$,
$\therefore \angle CAB = 60^{\circ}$.
$\because DB // AC$,$\therefore \angle DBA = 60^{\circ}$.
如图,过点D作$DE \perp AB$,垂足为点E.
设$BE = m(m > 0)$,则$DE = \sqrt{3}m$,$BD = 2m$,点D的坐标为$(2\sqrt{3} + \sqrt{3}m,2 - m)$.

$\because$点D为反比例函数$y = \frac{\sqrt{3}}{x}$图象上的一点,
$\therefore (2\sqrt{3} + \sqrt{3}m)(2 - m) = \sqrt{3}$,解得$m = \sqrt{3}$(负值舍去),
$\therefore BD = 2m = 2\sqrt{3}$,
$\therefore OB^{2} - BD^{2} = (2\sqrt{3})^{2} + 2^{2} - (2\sqrt{3})^{2} = 4$.
15. 核心素养·运算能力 先化简,再求值:$\frac{x^2 + 2x + 1}{x + 1}$,其中$x = \sqrt{2} - 1$。
答案:
15.[解析]本题考查分式化简求值.先根据分式的性质化简,最后将字母的值代入求解.
[解题过程]
解:原式$= \frac{(x + 1)^{2}}{x + 1} = x + 1$.(6分)
当$x = \sqrt{2} - 1$时,原式$= \sqrt{2} - 1 + 1 = \sqrt{2}$.(8分)
[解题过程]
解:原式$= \frac{(x + 1)^{2}}{x + 1} = x + 1$.(6分)
当$x = \sqrt{2} - 1$时,原式$= \sqrt{2} - 1 + 1 = \sqrt{2}$.(8分)
查看更多完整答案,请扫码查看


