第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1. $-5$的绝对值是(
A.$5$
B.$-5$
C.$-\dfrac{1}{5}$
D.$\dfrac{1}{5}$
A
)A.$5$
B.$-5$
C.$-\dfrac{1}{5}$
D.$\dfrac{1}{5}$
答案:
1.A 【解析】本题考查绝对值的意义.| - 5| = 5.
2. 据统计,2023年我国新能源汽车产量超过944万辆,其中944万用科学记数法表示为(
A.$0.944× 10^{7}$
B.$9.44× 10^{6}$
C.$9.44× 10^{7}$
D.$94.4× 10^{6}$
B
)A.$0.944× 10^{7}$
B.$9.44× 10^{6}$
C.$9.44× 10^{7}$
D.$94.4× 10^{6}$
答案:
2.B 【解析】本题考查科学记数法.
944万 = 9440000 = 9.44×10⁶.
944万 = 9440000 = 9.44×10⁶.
3. [核心素养·空间观念]某几何体的三视图如图所示,则该几何体为(

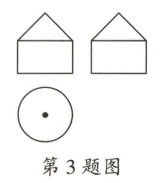
A.图A
B.图B
C.图C
D.图D
D
)

A.图A
B.图B
C.图C
D.图D
答案:
3.D 【解析】本题考查由三视图判断几何体.根据三视图的形状,结合三视图的定义以及几何体的形状特征可得该几何体为D选项.
4. 下列计算正确的是(
A.$a^{3}+a^{5}=a^{6}$
B.$a^{6}÷ a^{3}=a^{2}$
C.$(-a)^{2}=a^{2}$
D.$\sqrt{a^{2}}=a$
C
)A.$a^{3}+a^{5}=a^{6}$
B.$a^{6}÷ a^{3}=a^{2}$
C.$(-a)^{2}=a^{2}$
D.$\sqrt{a^{2}}=a$
答案:
4.C 【解析】本题考查合并同类项、同底数幂的除法、积的乘方运算、二次根式的性质等知识.
A选项,a³与a⁵不是同类项,不能合并,选项错误.B选项,a⁶÷a³ = a³,选项错误.C选项,( - a)² = a²,选项正确.D选项,$\sqrt{a^{2}}$ = a,当a≥0时,$\sqrt{a^{2}}$ = a,当a<0时,$\sqrt{a^{2}}$ = - a,选项错误.
【高分点拨】点拨:幂的运算性质
1.同底数幂相乘,底数不变,指数相加.
2.幂的乘方,底数不变,指数相乘.
3.积的乘方等于各因式乘方的积.
4.同底数幂相除,底数不变,指数相减.
5.一个非零数的零次方等于1.
A选项,a³与a⁵不是同类项,不能合并,选项错误.B选项,a⁶÷a³ = a³,选项错误.C选项,( - a)² = a²,选项正确.D选项,$\sqrt{a^{2}}$ = a,当a≥0时,$\sqrt{a^{2}}$ = a,当a<0时,$\sqrt{a^{2}}$ = - a,选项错误.
【高分点拨】点拨:幂的运算性质
1.同底数幂相乘,底数不变,指数相加.
2.幂的乘方,底数不变,指数相乘.
3.积的乘方等于各因式乘方的积.
4.同底数幂相除,底数不变,指数相减.
5.一个非零数的零次方等于1.
5. 若扇形$AOB$的半径为$6$,$\angle AOB=120^{\circ}$,则$\overset{\frown}{AB}$的长为(
A.$2\pi$
B.$3\pi$
C.$4\pi$
D.$6\pi$
C
)A.$2\pi$
B.$3\pi$
C.$4\pi$
D.$6\pi$
答案:
5.C 【解析】本题考查弧长公式.由题意可得,$\overset{\frown}{AB}$的长为$\frac{120\pi×6}{180}$ = 4π.
6. 已知反比例函数$y=\dfrac{k}{x}(k\neq 0)$与一次函数$y=2-x$的图象的一个交点的横坐标为$3$,则$k$的值为(
A.$-3$
B.$-1$
C.$1$
D.$3$
A
)A.$-3$
B.$-1$
C.$1$
D.$3$
答案:
6.A 【解析】本题考查一次函数与反比例函数的交点问题.
∵反比例函数y = $\frac{k}{x}$(k≠0)与一次函数y = 2 - x的图象的一个交点的横坐标为3,
∴y = 2 - 3 = - 1,
∴ - 1 = $\frac{k}{3}$,
∴k = - 3.
∵反比例函数y = $\frac{k}{x}$(k≠0)与一次函数y = 2 - x的图象的一个交点的横坐标为3,
∴y = 2 - 3 = - 1,
∴ - 1 = $\frac{k}{3}$,
∴k = - 3.
7. 如图,在$Rt\triangle ABC$中,$AC=BC=2$,点$D$在$AB$的延长线上,且$CD=AB$,则$BD$的长为(
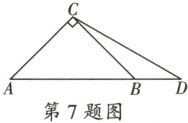
A.$\sqrt{10}-\sqrt{2}$
B.$\sqrt{6}-\sqrt{2}$
C.$2\sqrt{2}-2$
D.$2\sqrt{2}-\sqrt{6}$
B
)
A.$\sqrt{10}-\sqrt{2}$
B.$\sqrt{6}-\sqrt{2}$
C.$2\sqrt{2}-2$
D.$2\sqrt{2}-\sqrt{6}$
答案:
7.B 【解析】本题考查了等腰直角三角形的判定、性质和勾股定理.
如图,过点D作DE⊥CB的延长线于点E,则∠BED = 90°.

∵∠ACB = 90°,AC = BC = 2,
∴AB = $\sqrt{2^{2}+2^{2}}$ = 2$\sqrt{2}$,∠A = ∠ABC = 45°,
∴CD = 2$\sqrt{2}$,∠DBE = 45°,
∴△BDE为等腰直角三角形,
∴DE = BE.
设DE = BE = x,则CE = 2 + x.
在Rt△CDE中,CE² + DE² = CD²,
∴(2 + x)² + x² = (2$\sqrt{2}$)²,
解得x₁ = $\sqrt{3}$ - 1,x₂ = - $\sqrt{3}$ - 1(不合题意,舍去),
∴DE = BE = $\sqrt{3}$ - 1,
∴BD = $\sqrt{(\sqrt{3}-1)^{2}+(\sqrt{3}-1)^{2}}$ = $\sqrt{6}$ - $\sqrt{2}$.
7.B 【解析】本题考查了等腰直角三角形的判定、性质和勾股定理.
如图,过点D作DE⊥CB的延长线于点E,则∠BED = 90°.

∵∠ACB = 90°,AC = BC = 2,
∴AB = $\sqrt{2^{2}+2^{2}}$ = 2$\sqrt{2}$,∠A = ∠ABC = 45°,
∴CD = 2$\sqrt{2}$,∠DBE = 45°,
∴△BDE为等腰直角三角形,
∴DE = BE.
设DE = BE = x,则CE = 2 + x.
在Rt△CDE中,CE² + DE² = CD²,
∴(2 + x)² + x² = (2$\sqrt{2}$)²,
解得x₁ = $\sqrt{3}$ - 1,x₂ = - $\sqrt{3}$ - 1(不合题意,舍去),
∴DE = BE = $\sqrt{3}$ - 1,
∴BD = $\sqrt{(\sqrt{3}-1)^{2}+(\sqrt{3}-1)^{2}}$ = $\sqrt{6}$ - $\sqrt{2}$.
8. 已知实数$a$,$b$满足$a-b+1=0$,$0\lt a+b+1\lt 1$,则下列判断正确的是(
A.$-\dfrac{1}{2}\lt a\lt 0$
B.$\dfrac{1}{2}\lt b\lt 1$
C.$-2\lt 2a+4b\lt 1$
D.$-1\lt 4a+2b\lt 0$
C
)A.$-\dfrac{1}{2}\lt a\lt 0$
B.$\dfrac{1}{2}\lt b\lt 1$
C.$-2\lt 2a+4b\lt 1$
D.$-1\lt 4a+2b\lt 0$
答案:
8.C 【解析】本题考查等式的性质和不等式的性质.
∵a - b + 1 = 0,
∴a = b - 1.
∵0 < a + b + 1 < 1,
∴0 < b - 1 + b + 1 < 1,
∴0 < b < $\frac{1}{2}$,选项B错误,不符合题意.
∵a - b + 1 = 0,
∴b = a + 1.
∵0 < a + b + 1 < 1,
∴0 < a + a + 1 + 1 < 1,
∴ - 1 < a < - $\frac{1}{2}$,选项A错误,不符合题意.
∵ - 1 < a < - $\frac{1}{2}$,0 < b < $\frac{1}{2}$,
∴ - 2 < 2a < - 1,0 < 4b < 2,
∴ - 2 < 2a + 4b < 1,选项C正确,符合题意.
∵ - 1 < a < - $\frac{1}{2}$,0 < b < $\frac{1}{2}$,
∴ - 4 < 4a < - 2,0 < 2b < 1,
∴ - 4 < 4a + 2b < - 1,选项D错误,不符合题意.
∵a - b + 1 = 0,
∴a = b - 1.
∵0 < a + b + 1 < 1,
∴0 < b - 1 + b + 1 < 1,
∴0 < b < $\frac{1}{2}$,选项B错误,不符合题意.
∵a - b + 1 = 0,
∴b = a + 1.
∵0 < a + b + 1 < 1,
∴0 < a + a + 1 + 1 < 1,
∴ - 1 < a < - $\frac{1}{2}$,选项A错误,不符合题意.
∵ - 1 < a < - $\frac{1}{2}$,0 < b < $\frac{1}{2}$,
∴ - 2 < 2a < - 1,0 < 4b < 2,
∴ - 2 < 2a + 4b < 1,选项C正确,符合题意.
∵ - 1 < a < - $\frac{1}{2}$,0 < b < $\frac{1}{2}$,
∴ - 4 < 4a < - 2,0 < 2b < 1,
∴ - 4 < 4a + 2b < - 1,选项D错误,不符合题意.
9. 在凸五边形$ABCDE$中,$AB=AE$,$BC=DE$,点$F$是$CD$的中点.下列条件中,不能推出$AF$与$CD$一定垂直的是(
A.$\angle ABC=\angle AED$
B.$\angle BAF=\angle EAF$
C.$\angle BCF=\angle EDF$
D.$\angle ABD=\angle AEC$
D
)A.$\angle ABC=\angle AED$
B.$\angle BAF=\angle EAF$
C.$\angle BCF=\angle EDF$
D.$\angle ABD=\angle AEC$
答案:
9.D 【解析】本题考查全等三角形的判定和性质,等腰三角形“三线合一”性质.
A选项,如图,连接AC,AD.

∵∠ABC = ∠AED,AB = AE,BC = DE,
∴△ACB≌△ADE(SAS),
∴AC = AD.
又
∵点F为CD的中点,
∴AF⊥CD,故不符合题意.
B选项,如图,连接BF,EF.

∵AB = AE,∠BAF = ∠EAF,AF = AF,
∴△ABF≌△AEF(SAS),
∴BF = EF,
∠AFB = ∠AFE.
又
∵点F为CD的中点,
∴CF = DF.
∵BC = DE,
∴△CBF≌△DEF(SSS),
∴∠CFB = ∠DFE,
∴∠CFB + ∠AFB = ∠DFE + ∠AFE = 90°,
∴AF⊥CD,故不符合题意.
C选项,如图,连接BF,EF.

∵点F为CD的中点,
∴CF = DF.
∵∠BCF = ∠EDF,BC = DE,
∴△CBF≌△DEF(SAS),
∴BF = EF,∠CFB = ∠DFE.
∵AB = AE,AF = AF,
∴△ABF≌△AEF(SSS),
∴∠AFB = ∠AFE,
∴∠CFB + ∠AFB = ∠DFE + ∠AFE = 90°,
∴AF⊥CD,故不符合题意.
D选项,∠ABD = ∠AEC,无法得出相应结论,符合题意.
【高分点拨】点拨:几何问题的多结论判断题
解决此类问题的关键是根据不同的条件正确地画图,利用几何图形的性质解决问题,一般来说,正确结论之间有着相互联系或层层递进的关系,而错误的结论是独立的,与正确的结论没有任何联系.
9.D 【解析】本题考查全等三角形的判定和性质,等腰三角形“三线合一”性质.
A选项,如图,连接AC,AD.

∵∠ABC = ∠AED,AB = AE,BC = DE,
∴△ACB≌△ADE(SAS),
∴AC = AD.
又
∵点F为CD的中点,
∴AF⊥CD,故不符合题意.
B选项,如图,连接BF,EF.

∵AB = AE,∠BAF = ∠EAF,AF = AF,
∴△ABF≌△AEF(SAS),
∴BF = EF,
∠AFB = ∠AFE.
又
∵点F为CD的中点,
∴CF = DF.
∵BC = DE,
∴△CBF≌△DEF(SSS),
∴∠CFB = ∠DFE,
∴∠CFB + ∠AFB = ∠DFE + ∠AFE = 90°,
∴AF⊥CD,故不符合题意.
C选项,如图,连接BF,EF.

∵点F为CD的中点,
∴CF = DF.
∵∠BCF = ∠EDF,BC = DE,
∴△CBF≌△DEF(SAS),
∴BF = EF,∠CFB = ∠DFE.
∵AB = AE,AF = AF,
∴△ABF≌△AEF(SSS),
∴∠AFB = ∠AFE,
∴∠CFB + ∠AFB = ∠DFE + ∠AFE = 90°,
∴AF⊥CD,故不符合题意.
D选项,∠ABD = ∠AEC,无法得出相应结论,符合题意.
【高分点拨】点拨:几何问题的多结论判断题
解决此类问题的关键是根据不同的条件正确地画图,利用几何图形的性质解决问题,一般来说,正确结论之间有着相互联系或层层递进的关系,而错误的结论是独立的,与正确的结论没有任何联系.
查看更多完整答案,请扫码查看


