《2026年秒杀中考数学安徽专版》

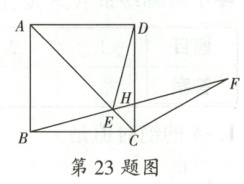
23. 如图，在正方形$ABCD$的对角线$AC$上取一点$E$，使得$\angle CDE = 15^{\circ}$，连接$BE$，并延长到点$F$，使得$CF = CB$，$BF$与$CD$相交于点$H$。
（1）求证：$BE = DE$。
（2）求证：$CE + DE = EF$。
（3）若$AB = 1$，求$\dfrac{DH}{HC}$的值。
 

答案：
23.解：
(1) 证明：
∵ 四边形ABCD是正方形,
∴ AB = AD, ∠ABC = ∠ADC = 90°, ∠BAC = ∠DAC = ∠ACB = ∠ACD = 45°.
在△ABE和△ADE中, $\begin{cases} AB = AD, \\ ∠BAC = ∠DAC, \\ AE = AE, \end{cases}$
∴ △ABE ≌ △ADE(SAS),
∴ BE = DE. (3分)
(2) 证明：在EF上取一点G, 使EG = EC, 连接CG.
∵ △ABE ≌ △ADE(SAS),
∴ ∠ABE = ∠ADE,
∴ ∠CBE = ∠CDE.
∵ BC = CF,
∴ ∠CBE = ∠F,
∴ ∠CBE = ∠CDE = ∠F.
∵ ∠CDE = 15°,
∴ ∠CBE = 15°,
∴ ∠CEG = ∠CBE + ∠ECB = 60°.
∵ CE = GE,
∴ △CEG是等边三角形,
∴ ∠CGE = 60°, CE = GC,
∴ ∠GCF = ∠EGC - ∠F = 45°,
∴ ∠ECD = ∠GCF = 45°.
∵ CF = CB, CB = CD,
∴ CD = CF.
在△DEC和△FGC中, $\begin{cases} CE = GC, \\ ∠ECD = ∠GCF, \\ CD = CF, \end{cases}$
∴ △DEC ≌ △FGC(SAS),
∴ DE = GF.
∵ EF = EG + GF,
∴ EF = CE + ED. (8分)
(3)过点D作DM ⊥ AC交于点M.

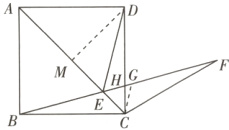
在Rt△ADC中, 根据勾股定理求出AC = $\sqrt{2}$.
由面积公式, 得$\frac{1}{2}$AD · DC = $\frac{1}{2}$AC · DM,
∴ DM = $\frac{\sqrt{2}}{2}$.
∵ ∠DCA = 45°,
∴ ∠AED = ∠EDC + ∠ACD = 60°,
∴ CM = MD = $\frac{\sqrt{2}}{2}$, EM = $\frac{1}{2}$ED.
在Rt△MED中, EM² = 4EM² - DM²,
∴ EM = $\frac{\sqrt{6}}{6}$,
∴ CE = CM - EM = $\frac{\sqrt{2}}{2} - \frac{\sqrt{6}}{6}$.
在Rt△MED中, DE = 2ME = $\frac{\sqrt{6}}{3}$.
∵ △ECG是等边三角形,
∴ CG = CE = $\frac{\sqrt{2}}{2} - \frac{\sqrt{6}}{6}$.
∵ ∠DEF = 180° - ∠AED - ∠GEC = 60° = ∠EGC, ∠DHE = ∠GHC,
∴ △DEH ∽ △CGH,
∴ $\frac{DH}{HC} = \frac{DE}{CG} = \frac{DE}{CE} = \frac{\sqrt{6}/3}{\sqrt{2}/2 - \sqrt{6}/6} = \sqrt{3} + 1$. (14分)