第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
9. 如图,在$\triangle ABC$中,$AD$,$BE$分别为边$BC$,$AC$上的高,$AD$,$BE$相交于点$F$,$AD = BD$,连接$CF$,则下列结论错误的是(
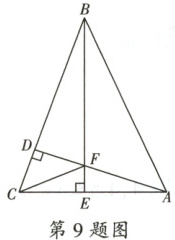
A.$BF = AC$
B.$\angle FCE + \angle BAE = 90^{\circ}$
C.$\angle FCD = \angle DAC$
D.若$BF = 2EC$,则$AB = BC$
C
)
A.$BF = AC$
B.$\angle FCE + \angle BAE = 90^{\circ}$
C.$\angle FCD = \angle DAC$
D.若$BF = 2EC$,则$AB = BC$
答案:
9.C 【解析】如图, 延长CF交AB于点H.

∵ AD, BE分别为边BC, AC上的高,
∴ ∠BDF = ∠ADC = ∠BEA = ∠BEC = 90°,
∴ ∠DAC + ∠ACB = ∠DBF + ∠ACB = 90°,
∴ ∠DAC = ∠DBF.
∵ AD = BD,
∴ ∠ABD = ∠BAD = 45°.
在△DBF和△DAC中,$\begin{cases} BD = AD, \\ ∠DBF = ∠DAC, \\ ∠BDF = ∠ADC = 90°, \end{cases}$
∴ △DBF≌△DAC(ASA),
∴ BF = AC, DF = DC,故A项正确,不符合题意;
∵ AD, BE分别为边BC, AC上的高,AD,BE相交于点F,CF的延长线交AB于点H,
∴ CH⊥AB,
∴ ∠FCE + ∠BAE = 90°.
故B项正确,不符合题意;
在△FDC中,∠FDC = 90°,DF = DC,
∴∠DFC = ∠FCD = 45°.
∵ ∠DFC>∠DAC,
∴∠FCD>∠DAC.
故C项错误,符合题意;
∵ BF = 2EC,BF = AC,
∴AC = 2EC,
∴AE = EC.
∵BE⊥AC,
∴BE垂直平分AC,
∴AB = BC.
故D项正确,不符合题意.
9.C 【解析】如图, 延长CF交AB于点H.

∵ AD, BE分别为边BC, AC上的高,
∴ ∠BDF = ∠ADC = ∠BEA = ∠BEC = 90°,
∴ ∠DAC + ∠ACB = ∠DBF + ∠ACB = 90°,
∴ ∠DAC = ∠DBF.
∵ AD = BD,
∴ ∠ABD = ∠BAD = 45°.
在△DBF和△DAC中,$\begin{cases} BD = AD, \\ ∠DBF = ∠DAC, \\ ∠BDF = ∠ADC = 90°, \end{cases}$
∴ △DBF≌△DAC(ASA),
∴ BF = AC, DF = DC,故A项正确,不符合题意;
∵ AD, BE分别为边BC, AC上的高,AD,BE相交于点F,CF的延长线交AB于点H,
∴ CH⊥AB,
∴ ∠FCE + ∠BAE = 90°.
故B项正确,不符合题意;
在△FDC中,∠FDC = 90°,DF = DC,
∴∠DFC = ∠FCD = 45°.
∵ ∠DFC>∠DAC,
∴∠FCD>∠DAC.
故C项错误,符合题意;
∵ BF = 2EC,BF = AC,
∴AC = 2EC,
∴AE = EC.
∵BE⊥AC,
∴BE垂直平分AC,
∴AB = BC.
故D项正确,不符合题意.
10. [核心素养·抽象能力]如图,在$Rt\triangle ABC$中,$\angle B = 90^{\circ}$,$\angle BAC = 30^{\circ}$,$AB = 3\sqrt{3}$,以3为边长的正方形$DEFG$的一边$GD$在直线$AB$上,且点$D$与点$A$重合,现将正方形$DEFG$沿$AB$的方向以每秒1个单位长度的速度向右匀速运动,当点$D$与点$B$重合时,停止运动。设在这个运动过程中,运动时间为$t\ s$,正方形$DEFG$与$\triangle ABC$的重合部分的面积为$S$,则$S$与$t$之间的函数关系图象大致是(

A.图A
B.图B
C.图C
D.图D
B
)
A.图A
B.图B
C.图C
D.图D
答案:
10.B 【解析】
∵ ∠B = 90°, ∠BAC = 30°, AB = 3$\sqrt{3}$,
∴ BC = 3.
当0 ≤ t ≤ 3时, S = $\frac{1}{2}$AD · DH = $\frac{1}{2} · \frac{t}{\sqrt{3}} · \frac{\sqrt{3}}{6}t^2$,为一个开口向上的抛物线的一部分;

当3 < t ≤ 3$\sqrt{3}$时, S = $\frac{1}{2} × 3(\frac{t}{\sqrt{3}} + \frac{t - 3}{\sqrt{3}}) = \frac{\sqrt{3}}{2}(2t - 3)$, 为一次函数, 图象为线段.
10.B 【解析】
∵ ∠B = 90°, ∠BAC = 30°, AB = 3$\sqrt{3}$,
∴ BC = 3.
当0 ≤ t ≤ 3时, S = $\frac{1}{2}$AD · DH = $\frac{1}{2} · \frac{t}{\sqrt{3}} · \frac{\sqrt{3}}{6}t^2$,为一个开口向上的抛物线的一部分;

当3 < t ≤ 3$\sqrt{3}$时, S = $\frac{1}{2} × 3(\frac{t}{\sqrt{3}} + \frac{t - 3}{\sqrt{3}}) = \frac{\sqrt{3}}{2}(2t - 3)$, 为一次函数, 图象为线段.
11. 若分式$\dfrac{x}{x + 6}$有意义,则实数$x$的取值范围是
x≠−6
。
答案:
11.x≠−6
12. [数学文化]我国南北朝时期数学家何承天发明的“调日法”便是利用分数的加成性质而设计的一种实数的有理逼近算法,使用一次“调日法”计算$\sqrt{5}$的一个更为精确的近似分数为$\dfrac{23}{10}$。请比较大小:$\sqrt{5}$
<
$\dfrac{23}{10}$(选填“$>$”或“$<$”)
答案:
12.<
13. 将标有“最”“美”“安”“徽”的四个小球装在一个不透明的口袋中(每个小球上仅标一个汉字),这些小球除所标汉字不同外,其余均相同。从中随机摸出一个球,放回后搅匀,再随机摸出一个球,则这两次摸到的球上的汉字可以组成“安徽”的概率是
$\frac{1}{8}$
。
答案:
13. $\frac{1}{8}$ 【解析】列表如下:
| | 最 | 美 | 安 | 徽 |
| --- | --- | --- | --- | --- |
| 最 | (最,最) | (最,美) | (最,安) | (最,徽) |
| 美 | (美,最) | (美,美) | (美,安) | (美,徽) |
| 安 | (安,最) | (安,美) | (安,安) | (安,徽) |
| 徽 | (徽,最) | (徽,美) | (徽,安) | (徽,徽) |
共有16种等可能的结果, 其中这两次摸到的球上的汉字可以组成“安徽”的结果有:(安, 徽), (徽, 安), 共2种,
∴ 这两次摸到的球上的汉字可以组成“安徽”的概率为$\frac{2}{16} = \frac{1}{8}$.
故答案为$\frac{1}{8}$.
| | 最 | 美 | 安 | 徽 |
| --- | --- | --- | --- | --- |
| 最 | (最,最) | (最,美) | (最,安) | (最,徽) |
| 美 | (美,最) | (美,美) | (美,安) | (美,徽) |
| 安 | (安,最) | (安,美) | (安,安) | (安,徽) |
| 徽 | (徽,最) | (徽,美) | (徽,安) | (徽,徽) |
共有16种等可能的结果, 其中这两次摸到的球上的汉字可以组成“安徽”的结果有:(安, 徽), (徽, 安), 共2种,
∴ 这两次摸到的球上的汉字可以组成“安徽”的概率为$\frac{2}{16} = \frac{1}{8}$.
故答案为$\frac{1}{8}$.
14. 如图1,在平面直角坐标系中,$Rt\triangle OAB$的直角边$OA$在$y$轴的正半轴上,且$OA = 6$,斜边$OB = 10$,$P$为线段$AB$上的一动点。
(1)点$B$的坐标为
(2)如图2,若$E$为线段$OB$的中点,连接$PE$,以$PE$为折痕,在平面内将$\triangle APE$折叠,点$A$的对应点为$A'$,当$PA'\perp OB$时,$\triangle APE$的面积为

(1)点$B$的坐标为
(8,6)
。(2)如图2,若$E$为线段$OB$的中点,连接$PE$,以$PE$为折痕,在平面内将$\triangle APE$折叠,点$A$的对应点为$A'$,当$PA'\perp OB$时,$\triangle APE$的面积为
$\frac{33}{4}$
。
答案:
14.
(1)(8,6)
(2)$\frac{33}{4}$ 【解析】
(1) 在Rt△AOB中, ∠OAB = 90°, OA = 6, OB = 10, 由勾股定理, 得AB = $\sqrt{OB^2 - OA^2} = \sqrt{10^2 - 6^2} = 8$,
∴ B(8,6). 故答案为(8,6).
(2)如图2, 设PA'交OB于点T.

∵ ∠OAB = 90°, OE = EB,
∴ EA = EO = EB = 5,
∴ ∠EAB = ∠B.
由翻折的性质可知∠EAB = ∠A',
∴ ∠A' = ∠B.
∵ A'P ⊥ OB,
∴ ∠ETA' = ∠BAO = 90°,
∴ △A'TE ∽ △BAO, △AOB ∽ △TPB,
∴ $\frac{A'E}{OB} = \frac{ET}{AO} = \frac{BT}{PB} = \frac{AB}{OB}$,
∴ $\frac{5}{10} = \frac{ET}{6}$,
∴ ET = 3, BT = 5 - 3 = 2.
∵ $\frac{BT}{PB} = \frac{AB}{OB}$,
∴ $\frac{2}{PB} = \frac{8}{10}$,
∴ PB = $\frac{5}{2}$, A'P = AP = AB - PB = 8 - $\frac{5}{2} = \frac{11}{2}$,
S△APE = S△A'PE = $\frac{1}{2}A'P · ET = \frac{1}{2} × \frac{11}{2} × 3 = \frac{33}{4}$.
故答案为$\frac{33}{4}$.
14.
(1)(8,6)
(2)$\frac{33}{4}$ 【解析】
(1) 在Rt△AOB中, ∠OAB = 90°, OA = 6, OB = 10, 由勾股定理, 得AB = $\sqrt{OB^2 - OA^2} = \sqrt{10^2 - 6^2} = 8$,
∴ B(8,6). 故答案为(8,6).
(2)如图2, 设PA'交OB于点T.

∵ ∠OAB = 90°, OE = EB,
∴ EA = EO = EB = 5,
∴ ∠EAB = ∠B.
由翻折的性质可知∠EAB = ∠A',
∴ ∠A' = ∠B.
∵ A'P ⊥ OB,
∴ ∠ETA' = ∠BAO = 90°,
∴ △A'TE ∽ △BAO, △AOB ∽ △TPB,
∴ $\frac{A'E}{OB} = \frac{ET}{AO} = \frac{BT}{PB} = \frac{AB}{OB}$,
∴ $\frac{5}{10} = \frac{ET}{6}$,
∴ ET = 3, BT = 5 - 3 = 2.
∵ $\frac{BT}{PB} = \frac{AB}{OB}$,
∴ $\frac{2}{PB} = \frac{8}{10}$,
∴ PB = $\frac{5}{2}$, A'P = AP = AB - PB = 8 - $\frac{5}{2} = \frac{11}{2}$,
S△APE = S△A'PE = $\frac{1}{2}A'P · ET = \frac{1}{2} × \frac{11}{2} × 3 = \frac{33}{4}$.
故答案为$\frac{33}{4}$.
查看更多完整答案,请扫码查看


