第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
21. [核心素养·数据观念]综合与实践
[项目背景] 无核柑橘是我省西南山区特产,该地区某村有甲、乙两块成龄无核柑橘园.在柑橘收获季节,班级同学前往该村开展综合实践活动,其中一个项目是:在日照、土质、空气湿度等外部环境基本一致的条件下,对两块柑橘园的优质柑橘情况进行调查统计,为柑橘园的发展规划提供一些参考.
[数据收集与整理] 从两块柑橘园采摘的柑橘中各随机选取$200$个,在技术人员指导下,测量每个柑橘的直径,作为样本数据,柑橘直径用$x$(单位:$cm$)表示.
将所收集的样本数据进行如下分组:

整理样本数据,并绘制甲、乙两园样本数据的频数直方图,部分信息如下:
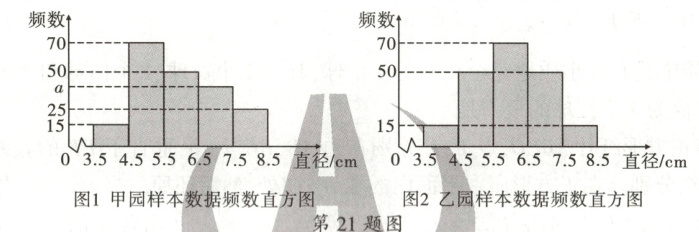
任务1 求图1中$a$的值.
[数据分析与运用]
任务2 $A$,$B$,$C$,$D$,$E$五组数据的平均数分别取为$4$,$5$,$6$,$7$,$8$.计算乙园样本数据的平均数.
任务3 下列结论一定正确的是(填正确结论的序号).
① 两园样本数据的中位数均在$C$组;
② 两园样本数据的众数均在$C$组;
③ 两园样本数据的最大数与最小数的差相等.
任务4 结合市场情况,将$C$,$D$两组的柑橘认定为一级,$B$组的柑橘认定为二级,其他组的柑橘认定为三级,其中一级柑橘的品质最优,二级次之,三级最次.试估计哪个园的柑橘品质更优,并说明理由.
根据所给信息,请完成以上所有任务.
[项目背景] 无核柑橘是我省西南山区特产,该地区某村有甲、乙两块成龄无核柑橘园.在柑橘收获季节,班级同学前往该村开展综合实践活动,其中一个项目是:在日照、土质、空气湿度等外部环境基本一致的条件下,对两块柑橘园的优质柑橘情况进行调查统计,为柑橘园的发展规划提供一些参考.
[数据收集与整理] 从两块柑橘园采摘的柑橘中各随机选取$200$个,在技术人员指导下,测量每个柑橘的直径,作为样本数据,柑橘直径用$x$(单位:$cm$)表示.
将所收集的样本数据进行如下分组:

整理样本数据,并绘制甲、乙两园样本数据的频数直方图,部分信息如下:

任务1 求图1中$a$的值.
[数据分析与运用]
任务2 $A$,$B$,$C$,$D$,$E$五组数据的平均数分别取为$4$,$5$,$6$,$7$,$8$.计算乙园样本数据的平均数.
任务3 下列结论一定正确的是(填正确结论的序号).
① 两园样本数据的中位数均在$C$组;
② 两园样本数据的众数均在$C$组;
③ 两园样本数据的最大数与最小数的差相等.
任务4 结合市场情况,将$C$,$D$两组的柑橘认定为一级,$B$组的柑橘认定为二级,其他组的柑橘认定为三级,其中一级柑橘的品质最优,二级次之,三级最次.试估计哪个园的柑橘品质更优,并说明理由.
根据所给信息,请完成以上所有任务.
答案:
21.解:任务1:a = 200 - 15 - 70 - 50 - 25 = 40.
(3分)
任务2:$\frac{15×4 + 50×5 + 70×6 + 50×7 + 15×8}{200}$ = 6,
乙园样本数据的平均数为6.(6分)
任务3:①
∵15 + 70 < 100,15 + 50 + 70 > 101,
∴甲园样本数据的中位数在C组.
∵15 + 50 < 100,15 + 50 + 70 > 101,
∴乙园样本数据的中位数在C组,故①正确;
②由样本数据频数直方图可知,甲园样本数据的众数均在B组,乙园样本数据的众数均在C组,故②错误;
③无法判断两园样本数据的最大数与最小数的差是否相等,故③错误.
故答案为①.(9分)
任务4:甲园样本数据的一级率为$\frac{50 + 40}{200}$×100% = 45%,
乙园样本数据的一级率为$\frac{70 + 50}{200}$×100% = 60%.
∵乙园样本数据的一级率高于甲园样本数据的一级率,
∴乙园的柑橘品质更优.(12分)
【高分点拨】点拨:平均数、中位数、众数与方差
1.平均数反映的是一组数据的平均水平,但容易受到极端数据的影响.
2.中位数反映的是一组数据的中等水平,将数据按从大到小或从小到大的顺序排好后,若数据为偶数个,则中间两数的平均数是这组数据的中位数;若数据为奇数个,则中间的数是这组数据的中位数.
3.众数反映的是一组数据的多数水平,一组数据中出现次数最多的数就是这组数据的众数,众数可能不止一个,也可能没有.
4.方差反映的是一组数据的波动情况,方差越大,稳定性越差,方差越小,稳定性越好.
(3分)
任务2:$\frac{15×4 + 50×5 + 70×6 + 50×7 + 15×8}{200}$ = 6,
乙园样本数据的平均数为6.(6分)
任务3:①
∵15 + 70 < 100,15 + 50 + 70 > 101,
∴甲园样本数据的中位数在C组.
∵15 + 50 < 100,15 + 50 + 70 > 101,
∴乙园样本数据的中位数在C组,故①正确;
②由样本数据频数直方图可知,甲园样本数据的众数均在B组,乙园样本数据的众数均在C组,故②错误;
③无法判断两园样本数据的最大数与最小数的差是否相等,故③错误.
故答案为①.(9分)
任务4:甲园样本数据的一级率为$\frac{50 + 40}{200}$×100% = 45%,
乙园样本数据的一级率为$\frac{70 + 50}{200}$×100% = 60%.
∵乙园样本数据的一级率高于甲园样本数据的一级率,
∴乙园的柑橘品质更优.(12分)
【高分点拨】点拨:平均数、中位数、众数与方差
1.平均数反映的是一组数据的平均水平,但容易受到极端数据的影响.
2.中位数反映的是一组数据的中等水平,将数据按从大到小或从小到大的顺序排好后,若数据为偶数个,则中间两数的平均数是这组数据的中位数;若数据为奇数个,则中间的数是这组数据的中位数.
3.众数反映的是一组数据的多数水平,一组数据中出现次数最多的数就是这组数据的众数,众数可能不止一个,也可能没有.
4.方差反映的是一组数据的波动情况,方差越大,稳定性越差,方差越小,稳定性越好.
查看更多完整答案,请扫码查看


