第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
9. 已知二次函数$ y = ax^2 + bx + c(a \neq 0) $的图象如图所示,则 (

A.$ abc < 0 $
B.$ 2a + b < 0 $
C.$ 2b - c < 0 $
D.$ a - b + c < 0 $
C
)
A.$ abc < 0 $
B.$ 2a + b < 0 $
C.$ 2b - c < 0 $
D.$ a - b + c < 0 $
答案:
9.C 【解析】本题考查二次函数图象与系数的关系。由图象可知抛物线交$x$轴于点$(2,0)$,另一个交点横坐标在-1和0之间。根据对称性可知对称轴$-\frac{1}{2} < -\frac{b}{2a} < 1$,$\therefore b > -2a$,即$2a + b > 0$,故B选项错误;当$x = -1$时,可知$y > 0$,即$a - b + c > 0$,故D选项错误;观察图象知$a > 0$,$b < 0$,$c < 0$,故$abc < 0$,故A选项错误;由对称轴的范围可知$b < -a$,即$b + a < 0$,故$4b + 4a < 0$ ①。把点$(2,0)$代入抛物线中,得$4a + 2b + c = 0$,故$4a = -2b - c$,再代入①式中,得$4b - 2b - c < 0$,整理即为$2b - c < 0$,故C选项正确。
10. 如图,在四边形$ ABCD $中,$ \angle A = \angle ABC = 90° $,$ AB = 4 $,$ BC = 3 $,$ AD = 1 $,点$ E $为边$ AB $上的动点.将线段$ DE $绕点$ D $逆时针旋转$ 90° $得到线段$ DF $,连接$ FB,FC,EC $,则下列结论错误的是 (
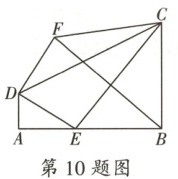
A.$ EC - ED $的最大值是$ 2\sqrt{5} $
B.$ FB $的最小值是$ \sqrt{10} $
C.$ EC + ED $的最小值是$ 4\sqrt{2} $
D.$ FC $的最大值是$ \sqrt{13} $
A
)
A.$ EC - ED $的最大值是$ 2\sqrt{5} $
B.$ FB $的最小值是$ \sqrt{10} $
C.$ EC + ED $的最小值是$ 4\sqrt{2} $
D.$ FC $的最大值是$ \sqrt{13} $
答案:
10.A 【解析】本题考查了旋转的性质、全等三角形的判定与性质、矩形的判定及性质、勾股定理以及几何最值问题。
$\because$将线段$DE$绕点$D$逆时针旋转$90°$得到线段$DF$,$\therefore DE = DF$,$\angle EDF = 90°$。
又$\because \angle A = \angle ABC = 90°$,$AB = 4$,$BC = 3$,$AD = 1$,过点$D$作$DG \perp BC$于点$G$,在$DG$上取一点$H$使得$DH = AD = 1$,延长$FH$交$AB$于点$I$,则四边形$ABGD$是矩形。

$\therefore \angle GDA = \angle ADE + \angle EDG = 90° = \angle EDG + \angle HDF$,$\therefore \angle ADE = \angle HDF$,$\therefore \triangle DHF \cong \triangle DAE(SAS)$,$\therefore \angle DHF = \angle DAE = 90°$,$\therefore FH \perp DG$,即点$F$在$FH$上运动。
四边形$DAIH$和四边形$BGHI$是矩形,$\therefore HI = AD = BG = 1$,$AI = DH = 1$,$BI = 4 - 1 = 3$。
$\because \angle A = \angle ABC = 90°$,$AB = 4$,$BC = 3$,$AD = 1$,$\therefore DE = \sqrt{1^2 + (4 - BE)^2}$,$CE = \sqrt{3^2 + BE^2}$,$\therefore EC - ED = \sqrt{3^2 + BE^2} - \sqrt{1^2 + (4 - BE)^2}$,$\therefore BE$最大时,$EC - ED$最大。
当点$E$与点$A$重合时,点$F$与点$H$重合,$FB$最小,此时$EC = \sqrt{4^2 + 3^2} = 5$,$ED = 1$,$EC - ED = 5 - 1 = 4 \neq 2\sqrt{5}$,故A项错误,符合题意。
$FB = \sqrt{HI^2 + BI^2} = \sqrt{1^2 + 3^2} = \sqrt{10}$,故B项正确,不符合题意。
作点$D$关于$AB$的对称点$M$,连接$MC$,$ME$,则$ED = EM$,$AD = AM = 1$,$\angle BAM = \angle BAD = 90°$,过点$M$作$MN \perp CB$交$CB$的延长线于点$N$,此时$EC + ED \geq CM$,当$C$,$E$,$M$三点共线时,$EC + ED$最小。

$\because MN \perp CB$,$\angle ABN = 180° - 90° = 90°$,$\therefore$四边形$AMNB$是矩形,$\therefore BN = AM = 1$,$CN = 3 + 1 = 4$,$AB = MN = 4$,$\therefore EC + ED$的最小值$= MC = \sqrt{4^2 + 4^2} = 4\sqrt{2}$,故C项正确,不符合题意。
当点$E$与点$A$重合时,$CF = \sqrt{GF^2 + CG^2} = \sqrt{(3 - 1)^2 + (4 - 1)^2} = \sqrt{13}$。
当点$E$与点$B$重合时,过点$C$作$CQ \perp FH$,则四边形$CQIB$是矩形。

$\therefore CQ = IB = 4 - 1 = 3$,$QI = BC = 3$。
$\because \triangle DHF \cong \triangle DAE$,$\therefore FH = AE = 4$,$\therefore QF = FH + HI - QI = 4 + 1 - 3 = 2$,$\therefore FC = \sqrt{CQ^2 + QF^2} = \sqrt{2^2 + 3^2} = \sqrt{13}$。
综上所述,$FC$的最大值为$\sqrt{13}$。故D项正确,不符合题意。
10.A 【解析】本题考查了旋转的性质、全等三角形的判定与性质、矩形的判定及性质、勾股定理以及几何最值问题。
$\because$将线段$DE$绕点$D$逆时针旋转$90°$得到线段$DF$,$\therefore DE = DF$,$\angle EDF = 90°$。
又$\because \angle A = \angle ABC = 90°$,$AB = 4$,$BC = 3$,$AD = 1$,过点$D$作$DG \perp BC$于点$G$,在$DG$上取一点$H$使得$DH = AD = 1$,延长$FH$交$AB$于点$I$,则四边形$ABGD$是矩形。

$\therefore \angle GDA = \angle ADE + \angle EDG = 90° = \angle EDG + \angle HDF$,$\therefore \angle ADE = \angle HDF$,$\therefore \triangle DHF \cong \triangle DAE(SAS)$,$\therefore \angle DHF = \angle DAE = 90°$,$\therefore FH \perp DG$,即点$F$在$FH$上运动。
四边形$DAIH$和四边形$BGHI$是矩形,$\therefore HI = AD = BG = 1$,$AI = DH = 1$,$BI = 4 - 1 = 3$。
$\because \angle A = \angle ABC = 90°$,$AB = 4$,$BC = 3$,$AD = 1$,$\therefore DE = \sqrt{1^2 + (4 - BE)^2}$,$CE = \sqrt{3^2 + BE^2}$,$\therefore EC - ED = \sqrt{3^2 + BE^2} - \sqrt{1^2 + (4 - BE)^2}$,$\therefore BE$最大时,$EC - ED$最大。
当点$E$与点$A$重合时,点$F$与点$H$重合,$FB$最小,此时$EC = \sqrt{4^2 + 3^2} = 5$,$ED = 1$,$EC - ED = 5 - 1 = 4 \neq 2\sqrt{5}$,故A项错误,符合题意。
$FB = \sqrt{HI^2 + BI^2} = \sqrt{1^2 + 3^2} = \sqrt{10}$,故B项正确,不符合题意。
作点$D$关于$AB$的对称点$M$,连接$MC$,$ME$,则$ED = EM$,$AD = AM = 1$,$\angle BAM = \angle BAD = 90°$,过点$M$作$MN \perp CB$交$CB$的延长线于点$N$,此时$EC + ED \geq CM$,当$C$,$E$,$M$三点共线时,$EC + ED$最小。

$\because MN \perp CB$,$\angle ABN = 180° - 90° = 90°$,$\therefore$四边形$AMNB$是矩形,$\therefore BN = AM = 1$,$CN = 3 + 1 = 4$,$AB = MN = 4$,$\therefore EC + ED$的最小值$= MC = \sqrt{4^2 + 4^2} = 4\sqrt{2}$,故C项正确,不符合题意。
当点$E$与点$A$重合时,$CF = \sqrt{GF^2 + CG^2} = \sqrt{(3 - 1)^2 + (4 - 1)^2} = \sqrt{13}$。
当点$E$与点$B$重合时,过点$C$作$CQ \perp FH$,则四边形$CQIB$是矩形。

$\therefore CQ = IB = 4 - 1 = 3$,$QI = BC = 3$。
$\because \triangle DHF \cong \triangle DAE$,$\therefore FH = AE = 4$,$\therefore QF = FH + HI - QI = 4 + 1 - 3 = 2$,$\therefore FC = \sqrt{CQ^2 + QF^2} = \sqrt{2^2 + 3^2} = \sqrt{13}$。
综上所述,$FC$的最大值为$\sqrt{13}$。故D项正确,不符合题意。
11. 计算:$ | - 5| - ( - 1) = $
6
$ $.
答案:
11.6 【解析】本题考查绝对值与有理数运算。原式$= 5 - (-1) = 6$。
12. 如图,$ AB $是$ \odot O $的弦,$ PB $与$ \odot O $相切于点$ B $,圆心$ O $在线段$ PA $上.已知$ \angle P = 50° $,则$ \angle PAB $的大小为$ $
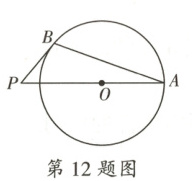
20°
$ $.
答案:
12.$20°$ 【解析】本题考查切线的性质、直角三角形的两个锐角互余、圆周角定理。
如图,连接$OB$。

$\because PB$与$\odot O$相切于点$B$,$\therefore PB \perp OB$,$\therefore \angle OBP = 90°$。
$\because \angle P = 50°$,$\therefore \angle POB = 90° - \angle P = 40°$,$\therefore \angle PAB = \frac{1}{2} \angle POB = 20°$。
故答案为$20°$。
12.$20°$ 【解析】本题考查切线的性质、直角三角形的两个锐角互余、圆周角定理。
如图,连接$OB$。

$\because PB$与$\odot O$相切于点$B$,$\therefore PB \perp OB$,$\therefore \angle OBP = 90°$。
$\because \angle P = 50°$,$\therefore \angle POB = 90° - \angle P = 40°$,$\therefore \angle PAB = \frac{1}{2} \angle POB = 20°$。
故答案为$20°$。
13. 跨学科·物理 在一个平衡的天平左、右两端托盘上,分别放置质量为20 g和70 g的物品后,天平倾斜(如图所示).现从质量为10 g,20 g,30 g,40 g的四件物品中,随机选取两件放置在天平的左端托盘上,则天平恢复平衡的概率为$ $

$\frac{1}{3}$
$ $.
答案:
13.$\frac{1}{3}$ 【解析】本题考查概率计算。由题意可知,$20 + 50 = 70(g)$,$10 + 40 = 20 + 30 = 50(g)$,把质量为$10g$,$20g$,$30g$,$40g$的四件物品分别记为$1$,$2$,$3$,$4$,画树状图如下:

共有$12$种等可能的结果,其中天平恢复平衡的结果有$4$种,$\therefore$天平恢复平衡的概率为$\frac{4}{12} = \frac{1}{3}$。
故答案为$\frac{1}{3}$。
【高分点拨】点拨:解决概率问题,通常用列表法或画树状图法,它们可以不重复、不遗漏地列出所有可能的结果。但是它们也有区别,列表法一般适用于两步完成的事件;树状图法一般适用于两步或两步以上完成的事件。根据列表或树状图来判断事件A有n种等可能的结果,事件A包含其中的m种结果,那么事件A发生的概率可表示为P(A)=$\frac{m}{n}$。另外用列表法或画树状图法分析所有可能的结果时要注意放回与不放回的区别。
13.$\frac{1}{3}$ 【解析】本题考查概率计算。由题意可知,$20 + 50 = 70(g)$,$10 + 40 = 20 + 30 = 50(g)$,把质量为$10g$,$20g$,$30g$,$40g$的四件物品分别记为$1$,$2$,$3$,$4$,画树状图如下:

共有$12$种等可能的结果,其中天平恢复平衡的结果有$4$种,$\therefore$天平恢复平衡的概率为$\frac{4}{12} = \frac{1}{3}$。
故答案为$\frac{1}{3}$。
【高分点拨】点拨:解决概率问题,通常用列表法或画树状图法,它们可以不重复、不遗漏地列出所有可能的结果。但是它们也有区别,列表法一般适用于两步完成的事件;树状图法一般适用于两步或两步以上完成的事件。根据列表或树状图来判断事件A有n种等可能的结果,事件A包含其中的m种结果,那么事件A发生的概率可表示为P(A)=$\frac{m}{n}$。另外用列表法或画树状图法分析所有可能的结果时要注意放回与不放回的区别。
14. 新考法 对于正整数$ n $,根据$ n $除以3的余数,分以下三种情况得到另一个正整数$ m $:若余数为0,则$ m = \frac{n}{3} $;若余数为1,则$ m = 2n $;若余数为2,则$ m = n + 1 $.这种得到$ m $的过程称为对$ n $进行一次变换.对所得的数$ m $再进行一次变换称为对$ n $进行二次变换,依此类推.例如,正整数$ n = 4 $,根据4除以3的余数为1,由$ 4 × 2 = 8 $知,对4进行一次变换得到的数为8;根据8除以3的余数为2,由$ 8 + 1 = 9 $知,对4进行二次变换得到的数为9;根据9除以3的余数为0,由$ 9 ÷ 3 = 3 $知,对4进行三次变换得到的数为3.
(1) 对正整数15进行三次变换,得到的数为$ $
(2) 若对正整数$ n $进行二次变换得到的数为1,则所有满足条件的$ n $的值之和为$ $
(1) 对正整数15进行三次变换,得到的数为$ $
2
$ $.(2) 若对正整数$ n $进行二次变换得到的数为1,则所有满足条件的$ n $的值之和为$ $
11
$ $.
答案:
14.
(1)$2$
(2)$11$ 【解析】本题考查新定义运算。
(1)$\because 15 ÷ 3 = 5 ·s ·s 0$,$\therefore 15$进行一次变换后得到的数为$\frac{15}{3} = 5$。
$\because 5 ÷ 3 = 1 ·s ·s 2$,$\therefore 15$进行二次变换后得到的数为$5 + 1 = 6$。
$\because 6 ÷ 3 = 2 ·s ·s 0$,$\therefore 15$进行三次变换后得到的数为$2$。
故答案为$2$。
(2)当对正整数$n$进行第一次变换后,所得的数除以$3$的余数为$0$时,则第一次变换后的数为$1 × 3 = 3$,此时符合题意;
当对正整数$n$进行第一次变换后,所得的数除以$3$的余数为$1$时,则第一次变换后的数为$\frac{1}{2}$,此时不符合题意;
当对正整数$n$进行第一次变换后,所得的数除以$3$的余数为$2$时,则第一次变换后的数为$1 - 1 = 0$,此时不符合题意。
综上所述,第一次变换后所得的数为$3$。
当$n$除以$3$的余数为$0$时,则$n = 3 × 3 = 9$,符合题意;
当$n$除以$3$的余数为$1$时,则$n = \frac{3}{2}$,不符合题意;
当$n$除以$3$的余数为$2$时,则$n = 3 - 1 = 2$,符合题意。
$\therefore$符合题意的$n$的值是$9$或$2$,
$\therefore$所有满足条件的$n$的值之和为$2 + 9 = 11$。
故答案为$11$。
(1)$2$
(2)$11$ 【解析】本题考查新定义运算。
(1)$\because 15 ÷ 3 = 5 ·s ·s 0$,$\therefore 15$进行一次变换后得到的数为$\frac{15}{3} = 5$。
$\because 5 ÷ 3 = 1 ·s ·s 2$,$\therefore 15$进行二次变换后得到的数为$5 + 1 = 6$。
$\because 6 ÷ 3 = 2 ·s ·s 0$,$\therefore 15$进行三次变换后得到的数为$2$。
故答案为$2$。
(2)当对正整数$n$进行第一次变换后,所得的数除以$3$的余数为$0$时,则第一次变换后的数为$1 × 3 = 3$,此时符合题意;
当对正整数$n$进行第一次变换后,所得的数除以$3$的余数为$1$时,则第一次变换后的数为$\frac{1}{2}$,此时不符合题意;
当对正整数$n$进行第一次变换后,所得的数除以$3$的余数为$2$时,则第一次变换后的数为$1 - 1 = 0$,此时不符合题意。
综上所述,第一次变换后所得的数为$3$。
当$n$除以$3$的余数为$0$时,则$n = 3 × 3 = 9$,符合题意;
当$n$除以$3$的余数为$1$时,则$n = \frac{3}{2}$,不符合题意;
当$n$除以$3$的余数为$2$时,则$n = 3 - 1 = 2$,符合题意。
$\therefore$符合题意的$n$的值是$9$或$2$,
$\therefore$所有满足条件的$n$的值之和为$2 + 9 = 11$。
故答案为$11$。
15. 核心素养·运算能力 先化简,再求值:$ \frac{2}{x^2 + 2x + 1} ÷ \frac{1}{x^2 - 1} $,其中$ x = 3 $.
答案:
15.解:$\frac{2}{x^2 + 2x + 1} ÷ \frac{1}{x^2 - 1}$
$=\frac{2}{(x + 1)^2} ÷ \frac{1}{(x + 1)(x - 1)}$
$=\frac{2}{(x + 1)^2} · (x + 1)(x - 1)$
$=\frac{2(x - 1)}{x + 1}$
$=\frac{2x - 2}{x + 1}$。(6分)
当$x = 3$时,原式$=\frac{2 × 3 - 2}{3 + 1} = \frac{4}{4} = 1$。(8分)
$=\frac{2}{(x + 1)^2} ÷ \frac{1}{(x + 1)(x - 1)}$
$=\frac{2}{(x + 1)^2} · (x + 1)(x - 1)$
$=\frac{2(x - 1)}{x + 1}$
$=\frac{2x - 2}{x + 1}$。(6分)
当$x = 3$时,原式$=\frac{2 × 3 - 2}{3 + 1} = \frac{4}{4} = 1$。(8分)
16. 如图,在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系$ xOy $,$ \triangle ABC $的顶点和$ A_1 $均为格点(网格线的交点).已知点$ A $和$ A_1 $的坐标分别为$ (-1,-3) $和$ (2,6) $.
(1) 在所给的网格图中描出边$ AB $的中点$ D $,并写出点$ D $的坐标.
(2) 以点$ O $为位似中心,将$ \triangle ABC $放大得到$ \triangle A_1B_1C_1 $,使得点$ A $的对应点为$ A_1 $,请在所给的网格图中画出$ \triangle A_1B_1C_1 $.

(1) 在所给的网格图中描出边$ AB $的中点$ D $,并写出点$ D $的坐标.
(2) 以点$ O $为位似中心,将$ \triangle ABC $放大得到$ \triangle A_1B_1C_1 $,使得点$ A $的对应点为$ A_1 $,请在所给的网格图中画出$ \triangle A_1B_1C_1 $.

答案:
16.解:
(1)如图所示,点$D$即为边$AB$的中点。

$\because A(-1,-3)$,$B(-3,1)$,$\therefore$点$D$的坐标为$(-2,-1)$。(4分)
(2)如图所示,$\triangle A_1B_1C_1$即为所求。(8分)
16.解:
(1)如图所示,点$D$即为边$AB$的中点。

$\because A(-1,-3)$,$B(-3,1)$,$\therefore$点$D$的坐标为$(-2,-1)$。(4分)
(2)如图所示,$\triangle A_1B_1C_1$即为所求。(8分)
查看更多完整答案,请扫码查看


