《2026年秒杀中考数学安徽专版》

19. [核心素养·几何直观]科技社团选择学校游泳池进行一次光的折射实验,如图,光线自点$B$处发出,经水面点$E$折射到池底点$A$处.已知$BE$与水平线的夹角$\alpha=36.9^{\circ}$,点$B$到水面的距离$BC=1.20\ m$,点$A$处水深为$1.20\ m$,到池壁的水平距离$AD=2.50\ m$,点$B$,$C$,$D$在同一条竖直线上,所有点都在同一竖直平面内.记入射角为$\beta$,折射角为$\gamma$,求$\dfrac{\sin\beta}{\sin\gamma}$的值.(结果精确到$0.1$,参考数据:$\sin 36.9^{\circ}\approx 0.60$,$\cos 36.9^{\circ}\approx 0.80$,$\tan 36.9^{\circ}\approx 0.75$)

答案：
19.解：如图，作EF⊥AD于点F，则∠AFE = 90°，DF = CE.

由题意，得∠BEC = ∠α = 36.9°，∠CBE = ∠β，
EF = 1.2m.
在Rt△BCE中，CE = $\frac{BC}{\tan\alpha}$ = $\frac{1.2}{0.75}$ = 1.6(m)，
BE = $\frac{BC}{\sin\alpha}$ ≈ $\frac{1.2}{0.6}$ = 2(m)，
∴sinβ = $\frac{CE}{BE}$ = $\frac{1.6}{2}$ = $\frac{4}{5}$，DF = 1.6m，(4分)
∴AF = AD - DF = 2.5 - 1.6 = 0.9(m)，
∴在Rt△AFE中，AE = $\sqrt{EF^{2}+AF^{2}}$ = $\sqrt{1.2^{2}+0.9^{2}}$ = 1.5(m)，
∴sinγ = $\frac{AF}{AE}$ = $\frac{0.9}{1.5}$ = $\frac{3}{5}$，(8分)
$\frac{\sin\beta}{\sin\gamma}$ = $\frac{\frac{4}{5}}{\frac{3}{5}}$ = $\frac{4}{3}$ ≈ 1.3.(10分)

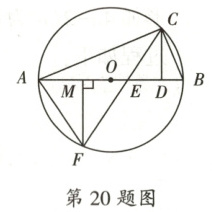
20. 如图,$\odot O$是$\triangle ABC$的外接圆,点$D$是直径$AB$上一点,$\angle ACD$的平分线交$AB$于点$E$,交$\odot O$于另一点$F$,$FA=FE$.
(1) 求证:$CD\perp AB$.
(2) 设$FM\perp AB$,垂足为点$M$.若$OM=OE=1$,求$AC$的长.

答案： 20.解：
(1)证明：
∵FA = FE，
∴∠FAE = ∠AEF.
又
∵∠FAE与∠BCE都是$\overset{\frown}{BF}$所对的圆周角，
∴∠FAE = ∠BCE.(2分)
∵∠AEF = ∠CEB，
∴∠CEB = ∠BCE.
∵CE平分∠ACD，
∴∠ACE = ∠DCE.
∵AB是直径，
∴∠ACB = 90°，
∴∠CEB + ∠DCE = ∠BCE + ∠ACE = ∠ACB = 90°，
故CD⊥AB.(5分)
(2)由
(1)知，∠CEB = ∠BCE，
∴BE = BC.
又
∵FA = FE，FM⊥AB，
∴MA = ME = MO + OE = 2，AE = 4，
∴OA = OB = AE - OE = 3，
∴BE = BC = OB - OE = 2.(8分)
在Rt△ABC中，AB = 2OA = 6，BC = 2，
∴AC = $\sqrt{AB^{2}-BC^{2}}$ = $\sqrt{6^{2}-2^{2}}$ = 4$\sqrt{2}$.(10分)