《2026年秒杀中考数学安徽专版》

15. 核心素养·运算能力 先化简，再求值：$\left(\dfrac{a}{a - 1} - 1\right) ÷ \dfrac{a^{2} + 2a + 1}{a^{2} - 1}$，其中$a = -\dfrac{1}{2}$。

答案： 15.解：原式 = $\frac{a-(a - 1)}{a - 1}$·$\frac{(a + 1)(a - 1)}{(a + 1)^{2}}$
= $\frac{1}{a - 1}$·$\frac{(a + 1)(a - 1)}{(a + 1)^{2}}$
= $\frac{1}{a + 1}$。(6分)
当a = -$\frac{1}{2}$时，原式 = $\frac{1}{-\frac{1}{2}+1}$ = 2。(8分)

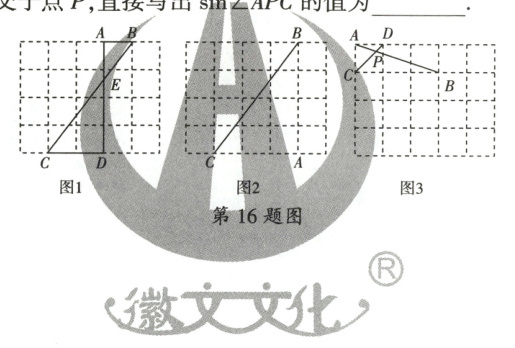
16. 如图均是$5×4$的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1，点$A$，$B$，$C$，$D$均在格点上。
(1)如图1，连接$AD$，$BC$交于点$E$，直接写出：$\dfrac{AE}{DE}$的值为\frac{1}{2}。
(2)如图2，在$BC$上找一点$F$，使$BF = 3$。(只用无刻度的直尺，在给定的正方形网格中，按要求画图，保留作图痕迹，不要求写画法)
(3)如图3，$AB$，$CD$相交于点$P$，直接写出$\sin \angle APC$的值为\frac{2\sqrt{5}}{5}。

答案：
16.解：
(1)由题意，得AB = 1，CD = 2，AB//CD，
∴△ABE∽△DCE，
∴$\frac{AE}{DE}$ = $\frac{AB}{CD}$ = $\frac{1}{2}$。
故答案为$\frac{1}{2}$。(2分)
(2)如图2，取格点D，E，使BD = 3，EC = 2，连接DE，交BC于点F，则点F即为所求。

由题意，得AC = 3，AB = 4，
∴BC = $\sqrt{AC^{2}+AB^{2}}$ = 5。
由题意，得DB = 3，CE = 2，DB//CE，
∴△DBF∽△ECF，
∴$\frac{BF}{CF}$ = $\frac{BD}{CE}$ = $\frac{3}{2}$，
∴$\frac{BF}{5 - BF}$ = $\frac{3}{2}$，
∴BF = 3。(4分)
(3)如图3，取格点F，E，使AE = AF = 4，点B在EF上，取格点G，连接AG。
　　　　　　
∵∠FAE = 90°，AE = AF，
∴∠AFE = ∠AEF = 45°。
∵AC = AD = 1，∠CAD = 90°，
∴∠ACD = ∠ADC = 45°，
∴CD//EF，
∴∠APC = ∠ABF。
由题意，得EG = FG = 2$\sqrt{2}$。
∵AE = AF，
∴AG⊥EF，
∴sin∠ABG = $\frac{AG}{AB}$。
∵AG = 2$\sqrt{2}$，AB = $\sqrt{1^{2}+3^{2}}$ = $\sqrt{10}$，
∴sin∠ABG = $\frac{AG}{AB}$ = $\frac{2\sqrt{2}}{\sqrt{10}}$ = $\frac{2\sqrt{5}}{5}$，
∴sin∠APC = $\frac{2\sqrt{5}}{5}$。
故答案为$\frac{2\sqrt{5}}{5}$。(8分)