《2026年秒杀中考数学安徽专版》

17. 新情境 某公司为庆祝新产品上市,在甲楼与乙楼的楼顶之间悬挂彩带营造喜庆气氛.如图所示,甲楼和乙楼分别用与水平地面垂直的线段$ AB $和$ CD $表示,彩带用线段$ AD $表示.工作人员在点$ A $处测得点$ C $的俯角为$ 23.8° $,测得点$ D $的仰角为$ 36.9° $.已知$ AB = 13.20 \, m $,求$ AD $的长.(结果精确到0.1 m,参考数据:$ \sin 23.8° \approx 0.40 $,$ \cos 23.8° \approx 0.91 $,$ \tan 23.8° \approx 0.44 $,$ \sin 36.9° \approx 0.60 $,$ \cos 36.9° \approx 0.80 $,$ \tan 36.9° \approx 0.75 $)
 

答案：
17.解：过点$A$作$AE \perp CD$，垂足为点$E$。

$\because$线段$AB$和$CD$都与地面垂直，$\therefore$四边形$ABCE$为矩形，$\therefore CE = AB = 13.20m$。(2分)
在$Rt \triangle ACE$中，$\tan \angle CAE = \frac{CE}{AE}$，$\therefore AE = \frac{CE}{\tan \angle CAE} = \frac{13.20}{\tan 23.8°} \approx \frac{13.20}{0.44} = 30.0(m)$。(5分)
在$Rt \triangle ADE$中，$\cos \angle DAE = \frac{AE}{AD}$，$\therefore AD = \frac{AE}{\cos \angle DAE} = \frac{30.0}{\cos 36.9°} \approx \frac{30.0}{0.80} = 37.5(m)$。
答：$AD$的长为$37.5m$。(8分)

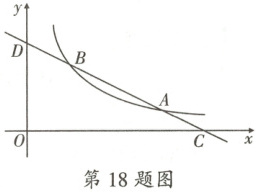
18. 如图,在平面直角坐标系$ xOy $中,一次函数$ y = ax + 4(a \neq 0) $与反比例函数$ y = \frac{k}{x}(k \neq 0) $的图象交于$ A,B $两点.已知点$ A $和点$ B $的横坐标分别为6和2.
(1) 求$ a $与$ k $的值.
(2) 设直线$ AB $与$ x $轴、$ y $轴的交点分别为$ C,D $,求$ \triangle COD $的面积.

答案： 18.解：
(1)由题意，得$\begin{cases}6a + 4 = \frac{k}{6}\\2a + 4 = \frac{k}{2}\end{cases}$，解得$a = -\frac{1}{2}$，$k = 6$。(4分)
(2)由
(1)知直线$AB$对应的一次函数解析式为$y = -\frac{1}{2}x + 4$。在$y = -\frac{1}{2}x + 4$中，令$y = 0$，得$x = 8$；令$x = 0$，得$y = 4$，$\therefore C(8,0)$，$D(0,4)$，$\therefore OC = 8$，$OD = 4$，$\therefore \triangle COD$的面积为$\frac{1}{2}OC · OD = \frac{1}{2} × 8 × 4 = 16$。(8分)

19. 核心素养·数据观念 某景区管理处为了解景区的服务质量,现从该景区5月份的游客中随机抽取50人对景区的服务质量进行评分,评分结果用$ x $表示(单位:分),将全部评分结果按以下五组进行整理,并绘制统计表,部分信息如下:
请根据以上信息,回答下列问题:
(1) $ a = $19$ $.
(2) 这50名游客对该景区服务质量评分的中位数落在$ $D$ $组.
(3) 若游客评分的平均数不低于75,则认定该景区的服务质量良好.分别用50,60,70,80,90作为A,B,C,D,E这五组评分的平均数,估计该景区5月份的服务质量是否良好,并说明理由.

答案： 19.解：
(1)$a = 50 - 3 - 3 - 15 - 10 = 19$。故答案为$19$。(3分)
(2)D (6分)
(3)$\bar{x} = \frac{1}{50} × (3 × 50 + 3 × 60 + 15 × 70 + 19 × 80 + 10 × 90)= 76$。
$\because 76 ＞ 75$，$\therefore$该景区$5$月份的服务质量良好。(10分)