《2026年秒杀中考数学安徽专版》

16. 根据经营情况，公司对某商品在甲、乙两地的销售单价进行了如下调整：甲地上涨10%，乙地降价5元。已知销售单价调整前甲地比乙地少10元，调整后甲地比乙地少1元，求调整前甲、乙两地该商品的销售单价。

答案： 16.[解析]本题考查二元一次方程组的应用，根据题意列出二元一次方程组是解题的关键.设调整前甲、乙两地该商品的销售单价分别为$x$，$y$元，根据题意，得$\begin{cases}x + 10 = y, \\x(1 + 10\%) + 1 = y - 5, \end{cases}$(5分)
解得$\begin{cases}x = 40, \\y = 50. \end{cases}$
答：调整前甲、乙两地该商品的销售单价分别为40,50元.(8分)

17. 如图，在由边长为1个单位长度的小正方形组成的网格中，点$A$，$B$，$C$，$D$均为格点（网格线的交点）。
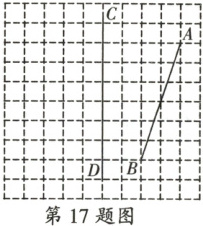
（1）画出线段$AB$关于直线$CD$对称的线段$A_1B_1$。
（2）将线段$AB$向左平移2个单位长度，再向上平移1个单位长度，得到线段$A_2B_2$，画出线段$A_2B_2$。
（3）描出线段$AB$上的点$M$及直线$CD$上的点$N$，使得直线$MN$垂直平分$AB$。

答案：
17.[解析]本题考查轴对称作图、平移作图、在网格图中作图问题.
(1)根据轴对称的性质，分别找到点A，B关于直线CD的对称点$A_1$，$B_1$，连接$A_1$，$B_1$，则线段$A_1B_1$即为所求.
(2)根据平移的性质得到线段$A_2B_2$即为所求.
(3)根据线段垂直平分线的作法画出图形即可.
[解题过程]
解：
(1)如图 所示，线段$A_1B_1$即为所求.(2分)
(2)如图所示，线段$A_2B_2$即为所求.(4分)
(3)如图所示，点M，N即为所求.(8分)
【高分点拨】 点拨：网格作图的解题通法
网格中图形的变换作图题，一般涉及平移、对称、旋转、位似等.
1.图形的对称
轴对称：
(1)找出原图形的关键点.
(2)作出关键点的对应点（关于$x$轴对称，横坐标相等，纵坐标互为相反数；关于$y$轴对称，纵坐标相等，横坐标互为相反数）.
(3)按照原图形依次连接得到的各关键点的对应点，得到对称后的图形.
中心对称：
(1)找出原图形的关键点.
(2)作出关键点的对应点（以关键点为中心，旋转$180^{\circ}$）.
(3)按照原图形依次连接得到的各关键点的对应点，得到对称后的图形.
2.图形的平移
(1)确定平移的方向和平移的距离.
(2)找出原图形的关键点，确定平移后的各对应点.其中横坐标左减右加，纵坐标上加下减.
(3)按照原图形依次连接得到的各关键点的对应点，即可得到平移后的图形.
3.图形的旋转
(1)确定旋转方向，旋转中心及旋转角度.
(2)找出原图形的关键点.
(3)确定旋转后的各关键点的对应点.
(4)按照原图形依次连接得到的各关键点的对应点，即可得到旋转后的图形.
4.图形的位似
(1)确定位似中心.
(2)确定原图形的关键点.
(3)确定位似比，即要将图形放大或缩小的倍数.
(4)确定各关键点的对应点.
(5)按照原图形依次连接得到的各关键点的对应点，即可得到所求位似图形.

18. 核心素养·推理能力 【观察思考】

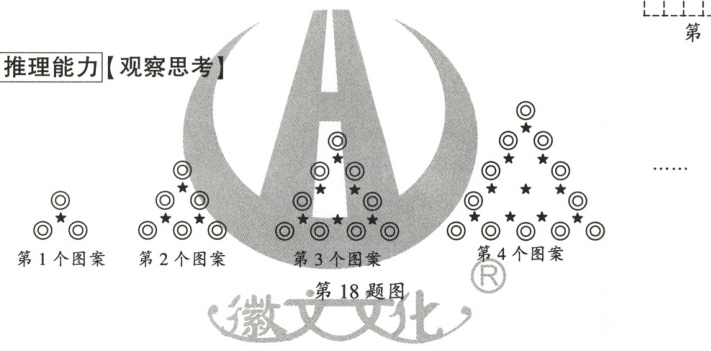
【规律发现】
请用含$n$的式子填空：
(1)第$n$个图案中“$\odot$”的个数为$$3n$$。
(2)第1个图案中“$\bigstar$”的个数可表示为$\frac{1 × 2}{2}$，第2个图案中“$\bigstar$”的个数可表示为$\frac{2 × 3}{2}$，第3个图案中“$\bigstar$”的个数可表示为$\frac{3 × 4}{2}$，第4个图案中“$\bigstar$”的个数可表示为$\frac{4 × 5}{2}·s·s$则第$n$个图案中“$\bigstar$”的个数可表示为$$\frac{n(n + 1)}{2}$$。
【规律应用】
(3)结合图案中“$\bigstar$”的排列方式及上述规律，求正整数$n$，使得连续的正整数之和$1 + 2 + 3 + ·s + n$等于第$n$个图案中“$\odot$”的个数的2倍。

答案： 18.[解析]本题考查图形规律探索.
(1)依次数出前4个图案中“◎”的个数，发现“◎”的个数与图案序号两者的关系，用代数式表示出来即可
(2)观察前4个图案中“★”的个数表达式与图案序号两者的关系，用代数式表示出来即可.
(3)观察前4个图案中“★”的个数，不难发现$1 + 2 + 3 + ·s + n$表示第n个图案中“★”的个数，
结合第
(2)问，则$1 + 2 + 3 + ·s + n = \frac{n(n + 1)}{2}$，列方程求解即可.
[解题过程]
解：
(1)$3n$(2分)
(2)$\frac{n(n + 1)}{2}$(4分)
(3)第n个图案中“★”的个数为$1 + 2 + 3 + ·s + n = \frac{n(n + 1)}{2}$.
根据题意，得$\frac{n(n + 1)}{2} = 3n × 2$，解得$n = 0$(舍去)或$n = 11$.(8分)