2025年聚能闯关期末复习冲刺卷八年级数学上册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年聚能闯关期末复习冲刺卷八年级数学上册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
8. 德力格尔草原位于彰武县境内,以草场资源丰富,景色优美著称。某年5月在此举办的“漠上草原欢乐跑”首届马拉松比赛,吸引了千余名国内外选手参加,甲、乙两名选手同时参加了往返$10km$(单程$5km$)的业余组比赛。如果全程保持匀速,甲、乙之间的距离$s(km)$与甲所用的时间$t(h)$之间的函数关系如图,那么当甲到达终点时,乙距离终点还有
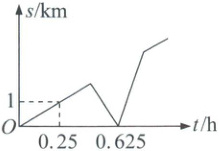
4
$km$。
答案:
8.4
1. (8分)已知点$A(a,3)$,$B(-4,b)$,试根据下列条件分别求出$a$,$b$的值。
(1)$A$,$B$两点关于$y$轴对称;
(2)$AB// x$轴,且线段$AB = 3$。
(1)$A$,$B$两点关于$y$轴对称;
(2)$AB// x$轴,且线段$AB = 3$。
答案:
1.解:
(1)
∵点$A(a,3)$,$B(- 4,b)$,$A$,$B$两点关于$y$轴对称,
∴$b = 3$,$a = 4$。
(2)
∵点$A(a,3)$,$B(- 4,b)$,线段$AB //$
$x$轴,且线段$AB = 3$,
∴$b = 3$,$\vert a - (- 4)\vert = 3$。
解得$a = - 1$或$- 7$。
(1)
∵点$A(a,3)$,$B(- 4,b)$,$A$,$B$两点关于$y$轴对称,
∴$b = 3$,$a = 4$。
(2)
∵点$A(a,3)$,$B(- 4,b)$,线段$AB //$
$x$轴,且线段$AB = 3$,
∴$b = 3$,$\vert a - (- 4)\vert = 3$。
解得$a = - 1$或$- 7$。
2. (8分)已知$y + 3$与$x + 2$成正比例,且当$x = 2$时,$y = 7$。
(1)求$y$与$x$的函数关系式;
(2)将所得函数图象向上平移3个单位长度,求平移后直线与坐标轴围成的三角形的面积。
(1)求$y$与$x$的函数关系式;
(2)将所得函数图象向上平移3个单位长度,求平移后直线与坐标轴围成的三角形的面积。
答案:
2.解:
(1)设$y + 3 = k(x + 2)$,
把$x = 2$,$y = 7$代入,得$7 + 3 = 4k$,即$k = \frac{5}{2}$。
∴$y$与$x$的函数关系式为$y + 3 = \frac{5}{2}(x + 2)$,即
$y = \frac{5}{2}x + 2$。
(2)将直线$y = \frac{5}{2}x + 2$向上平移$3$个单位长度
后得到的直线是$y = \frac{5}{2}x + 5$。
∴当$y = 0$时,$x = - 2$;当$x = 0$时,$y = 5$。
∴平移后的直线与$x$轴交点的坐标是$(- 2$,
$0)$,与$y$轴交点的坐标是$(0,5)$,
∴平移后的直线与两坐标轴围成的三角形的
面积是$\frac{1}{2} × 2 × 5 = 5$。
(1)设$y + 3 = k(x + 2)$,
把$x = 2$,$y = 7$代入,得$7 + 3 = 4k$,即$k = \frac{5}{2}$。
∴$y$与$x$的函数关系式为$y + 3 = \frac{5}{2}(x + 2)$,即
$y = \frac{5}{2}x + 2$。
(2)将直线$y = \frac{5}{2}x + 2$向上平移$3$个单位长度
后得到的直线是$y = \frac{5}{2}x + 5$。
∴当$y = 0$时,$x = - 2$;当$x = 0$时,$y = 5$。
∴平移后的直线与$x$轴交点的坐标是$(- 2$,
$0)$,与$y$轴交点的坐标是$(0,5)$,
∴平移后的直线与两坐标轴围成的三角形的
面积是$\frac{1}{2} × 2 × 5 = 5$。
3. (8分)如图,直线$AB$与$x$轴交于点$A(1,0)$,与$y$轴交于点$B(0,-2)$。
(1)求直线$AB$的解析式;
(2)若直线$AB$上的点$C$在第一象限,且$S_{\triangle BOC} = 2$,求点$C$的坐标。
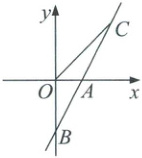
(1)求直线$AB$的解析式;
(2)若直线$AB$上的点$C$在第一象限,且$S_{\triangle BOC} = 2$,求点$C$的坐标。

答案:
3.解:
(1)设直线$AB$的解析式为$y = kx + b(k \neq 0)$。
∵直线$AB$过点$A(1,0)$,$B(0, - 2)$,
$\begin{cases}k + b = 0,\\b = - 2.\end{cases}$解得$\begin{cases}k = 2,\\b = - 2.\end{cases}$
∴直线$AB$的解析式为$y = 2x - 2$。
(2)
∵$B(0, - 2)$,
∴$OB = 2$。
∵$S_{\triangle BOC} = 2$,
∴点$C$的横坐标为$2$。
把$x = 2$代入$y = 2x - 2$,得$y = 2$,
∴点$C$的坐标为$(2,2)$。
(1)设直线$AB$的解析式为$y = kx + b(k \neq 0)$。
∵直线$AB$过点$A(1,0)$,$B(0, - 2)$,
$\begin{cases}k + b = 0,\\b = - 2.\end{cases}$解得$\begin{cases}k = 2,\\b = - 2.\end{cases}$
∴直线$AB$的解析式为$y = 2x - 2$。
(2)
∵$B(0, - 2)$,
∴$OB = 2$。
∵$S_{\triangle BOC} = 2$,
∴点$C$的横坐标为$2$。
把$x = 2$代入$y = 2x - 2$,得$y = 2$,
∴点$C$的坐标为$(2,2)$。
4. (12分)下图中标明了李明同学家附近的一些地方。
(1)根据图中所建立的平面直角坐标系,写出学校和邮局的坐标;
(2)星期天早晨,李明同学从家出发,沿着$(-2,-1)$,$(-1,-2)$,$(1,-2)$,$(2,-1)$,$(1,-1)$,$(1,3)$,$(-1,0)$,$(0,-1)$的路线转了一下,写出他路上经过的地方;
(3)连结他在(2)中经过的地点,你能得到什么图形?
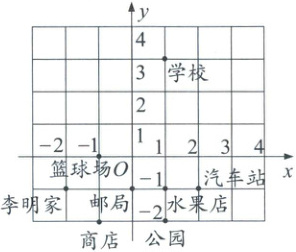
(1)根据图中所建立的平面直角坐标系,写出学校和邮局的坐标;
(2)星期天早晨,李明同学从家出发,沿着$(-2,-1)$,$(-1,-2)$,$(1,-2)$,$(2,-1)$,$(1,-1)$,$(1,3)$,$(-1,0)$,$(0,-1)$的路线转了一下,写出他路上经过的地方;
(3)连结他在(2)中经过的地点,你能得到什么图形?

答案:
4.解:
(1)学校$(1,3)$,邮局$(0, - 1)$。
(2)李明家、商店、公园、汽车站、水果店、
学校、篮球场、邮局。
(3)一只小船。
(1)学校$(1,3)$,邮局$(0, - 1)$。
(2)李明家、商店、公园、汽车站、水果店、
学校、篮球场、邮局。
(3)一只小船。
查看更多完整答案,请扫码查看


