2025年聚能闯关期末复习冲刺卷八年级数学上册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年聚能闯关期末复习冲刺卷八年级数学上册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
19. 下列描述属于定义的是(
A.三角形两边之和大于第三边
B.两点之间线段最短
C.含有未知数的等式叫作方程
D.三角形的中线是一条线段
C
)A.三角形两边之和大于第三边
B.两点之间线段最短
C.含有未知数的等式叫作方程
D.三角形的中线是一条线段
答案:
19.C
20. “垂直于同一条直线的两条直线互相平行”的题设是(
A.垂直
B.两条直线
C.同一条直线
D.两条直线垂直于同一条直线
D
)A.垂直
B.两条直线
C.同一条直线
D.两条直线垂直于同一条直线
答案:
20.D
21. 下列命题中:①对顶角相等;②同位角相等;③同一平面内,如果直线$l_1$//$l_2$,直线$l_1$//$l_3$,那么$l_2$//$l_3$;④同一平面内,如果直线$l_1$//$l_2$,直线$l_1$⊥$l_3$,那么$l_2$⊥$l_3$;⑤同一平面内,如果直线$l_1$与$l_2$相交,直线$l_1$与$l_3$相交,那么$l_2$与$l_3$相交。属于真命题的是
①③④
。(填序号)
答案:
21.①③④
22. 将命题“过直线外一点有且只有一条直线与已知直线垂直”改写成“如果……那么……”的形式:
如果直线外有一点,那么过这一点有且只有一条直线与这条直线垂直
。
答案:
22.如果直线外有一点,那么过这一点有且只有一条直线与这条直线垂直
23. 命题“若$|a| > |b|$,则$a > b$”是
假
命题。(填“真”或“假”)
答案:
23.假
24. 命题“等角的余角相等”的题设是
两个角是等角的余角
,结论是它们相等
。
答案:
24.两个角是等角的余角 它们相等
25. 请判断下列命题的真假,若是假命题,请举反例说明。
(1)若$a > b$,则$a^2 > b^2$;
(2)若三条线段$a$,$b$,$c$满足$a + b > c$,则这三条线段$a$,$b$,$c$能组成三角形。
(1)若$a > b$,则$a^2 > b^2$;
(2)若三条线段$a$,$b$,$c$满足$a + b > c$,则这三条线段$a$,$b$,$c$能组成三角形。
答案:
25.
(1)假命题,例如:0>-1,但0²<(-1)²。
(2)假命题,例如:三条线段a=3,b=2,c=1满足a+b>c,但这三条线段不能组成三角形。
(1)假命题,例如:0>-1,但0²<(-1)²。
(2)假命题,例如:三条线段a=3,b=2,c=1满足a+b>c,但这三条线段不能组成三角形。
26. 能作为证明依据的是(
A.已知条件
B.定义及基本事实
C.定理及推论
D.以上三项都对
D
)A.已知条件
B.定义及基本事实
C.定理及推论
D.以上三项都对
答案:
26.D
27. 如图,下面的推理正确的是(
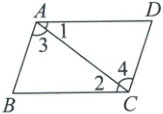
A.∵∠1 = ∠2,∴AB//CD
B.∵∠ABC + ∠BCD = 180°,∴AD//BC
C.∵AD//BC,∴∠3 = ∠4
D.∵∠ABC + ∠DAB = 180°,∴AD//BC
D
)
A.∵∠1 = ∠2,∴AB//CD
B.∵∠ABC + ∠BCD = 180°,∴AD//BC
C.∵AD//BC,∴∠3 = ∠4
D.∵∠ABC + ∠DAB = 180°,∴AD//BC
答案:
27.D
28. 完成下面的证明过程。
已知:如图,AB//CD,∠1 + ∠2 = 180°。
求证:CD//EF。
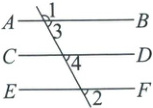
证明:∵∠1 + ∠3 = 180°(
∴∠3 = ∠2(
∵AB//CD(
∴∠3 = ∠4(
∴∠2 = ∠4。
∴CD//EF(
已知:如图,AB//CD,∠1 + ∠2 = 180°。
求证:CD//EF。

证明:∵∠1 + ∠3 = 180°(
平角的定义
),∠1 + ∠2 = 180°(已知
),∴∠3 = ∠2(
同角的补角相等
)。∵AB//CD(
已知
),∴∠3 = ∠4(
两直线平行,同位角相等
)。∴∠2 = ∠4。
∴CD//EF(
同位角相等,两直线平行
)。
答案:
28.平角的定义 已知 同角的补角相等 已知 两直线平行,同位角相等 同位角相等,两直线平行
查看更多完整答案,请扫码查看


