《2025年聚能闯关期末复习冲刺卷八年级数学上册浙教版》

4. （9分）如图，BD是∠ABC的平分线，AB = BC，点P在BD上，PM⊥AD，PN⊥CD，垂足分别是M，N。试说明：PM = PN。

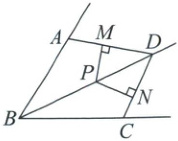
答案： 4.证明:
∵BD为∠ABC的平分线，
∴∠ABD=∠CBD。
　　　在△ABD和△CBD中，$\begin{cases}AB=CB,\\∠ABD=∠CBD,\\BD=BD,\end{cases}$
∴△ABD≌△CBD(SAS)。
∴∠ADB=∠CDB。
∵点P在BD上，PM⊥AD，PN⊥CD,
∴PM=PN。

5. （10分）如图，在下面四个条件中：①AE = AD，②AB = AC，③MB = MC，④∠B = ∠C，请你以其中的两个作为条件，第三个作为结论，写出一个正确的命题，并说明你的理由。

答案： 5.(答案不唯一)解:条件:①AE=AD,②AB=AC,结论:④∠B=∠C。
　　　证明:在△ADC和△AEB中，$\begin{cases}AD=AE,\\∠A=∠A,\\AC=AB,\end{cases}$
∴△ADC≌△AEB(SAS)。
∴∠B=∠C。

6. （12分）如图，点A，B，C，D在同一条直线上，点E，F分别在直线AB的两侧，且AE = BF，∠A = ∠B，∠ACE = ∠BDF。
（1）求证：△ACE≌△BDF；
（2）若AB = 8，AC = 2，求CD的长。

答案： 6.
(1)证明:在△ACE和△BDF中，$\begin{cases}∠ACE=∠BDF,\\∠A=∠B,\\AE=BF,\end{cases}$
∴△ACE≌△BDF(AAS)。
(2)解:由
(1)知△ACE≌△BDF。
∵AC=2,
∴BD=AC=2。
∵AB=8,
∴CD=AB−AC−BD=4。

7. （14分）如图，AD是△ABC的中线，DE是△ADC的中线，EF是△DEC的中线，FG是△EFC的中线。
（1）△ABD与△ADC的面积有何关系？请说明理由。
（2）若△GFC的面积为1 cm²，求△ABC的面积。

答案： 7.解:
(1)△ABD与△ADC的面积相等。理由:
∵AD是△ABC的中线，
∴BD=DC。
∵△ABD 和△ADC的底边分别为BD,DC，而且它们的高相同，即两个三角形等底等高，因此面积相等。
(2)由
(1)可知三角形的中线等分三角形的面积，$S_{\triangle GFC}=\frac{1}{16}S_{\triangle ABC}=1$，
∴△ABC的面积为16cm²。