9. 小彬用 3D 打印机制作了一个底面周长为 30 cm,高为 20 cm 的圆柱粮仓模型,$ BC $ 是底面直径,$ AB $ 是高。现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过 $ A $,$ C $ 两点(接头不计),则装饰带的长度最短为
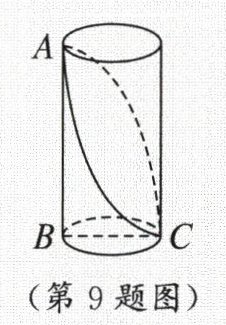
50 cm
。
答案:
9.50 cm
10. 如图,点 $ A $,$ B $,$ C $ 都在方格线的交点上,则 $ \angle ACB $ 的度数是
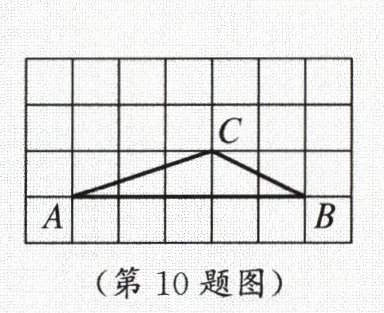
135°
。
答案:
10.135°
11. 如图,在 $ \triangle ABC $ 中,分别以点 $ A $ 和点 $ C $ 为圆心,大于 $ \frac{1}{2}AC $ 的长为半径作弧(弧所在圆的半径都相等),两弧相交于 $ M $,$ N $ 两点,直线 $ MN $ 分别与边 $ BC $,$ AC $ 相交于点 $ D $,$ E $,连接 $ AD $。若 $ BD = DC $,$ AE = 4 $,$ AD = 5 $,则 $ AB $ 的长为
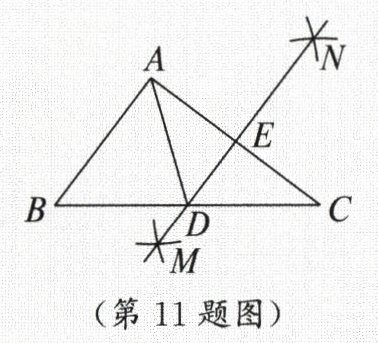
6
。
答案:
11.6
12. 如图,正方形 $ ABCD $ 的边长为 1,其面积标记为 $ S_{1} $,以 $ CD $ 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为 $ S_{2} $……按照此规律继续下去,则 $ S_{2025} $ 的值为
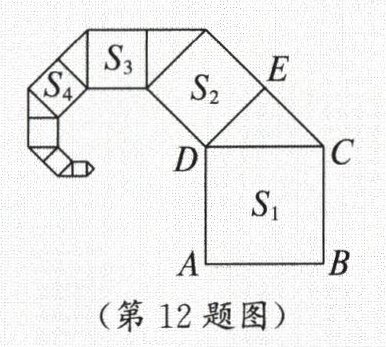
$\frac{1}{2^{2024}}$
。
答案:
12.$\frac{1}{2^{2024}}$
13. (8 分)如图,在长方形 $ ABCD $ 中,$ AB = 9 $,$ AD = 12 $。
(1)求对角线 $ AC $ 的长;
(2)点 $ E $ 是线段 $ CD $ 上的一点,把 $ \triangle ADE $ 沿着直线 $ AE $ 折叠,点 $ D $ 恰好落在线段 $ AC $ 上,与点 $ F $ 重合,求线段 $ DE $ 的长。
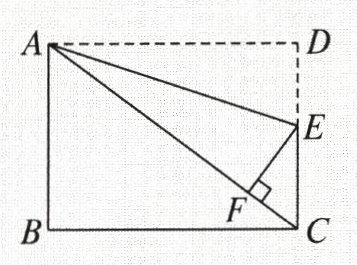
(1)求对角线 $ AC $ 的长;
(2)点 $ E $ 是线段 $ CD $ 上的一点,把 $ \triangle ADE $ 沿着直线 $ AE $ 折叠,点 $ D $ 恰好落在线段 $ AC $ 上,与点 $ F $ 重合,求线段 $ DE $ 的长。

答案:
13.解
(1)由题意可知AB=CD=9,AD=BC=12,所以AC²=AB²+BC²=9²+12²=15²,所以AC=15。
(2)因为把△ADE沿着直线AE折叠,点D恰好落在线段AC上,与点F重合,所以AF=AD=BC=12,DE=EF,FC=AC - AF=15 - 12=3。设DE=x,则EC=CD - DE=9 - x,EF=DE=x。因为EF²+FC²=EC²,所以x²+3²=(9 - x)²,解得x=4,即DE=4。
(1)由题意可知AB=CD=9,AD=BC=12,所以AC²=AB²+BC²=9²+12²=15²,所以AC=15。
(2)因为把△ADE沿着直线AE折叠,点D恰好落在线段AC上,与点F重合,所以AF=AD=BC=12,DE=EF,FC=AC - AF=15 - 12=3。设DE=x,则EC=CD - DE=9 - x,EF=DE=x。因为EF²+FC²=EC²,所以x²+3²=(9 - x)²,解得x=4,即DE=4。
查看更多完整答案,请扫码查看


