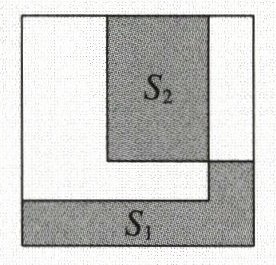
14. (10 分)已知直角三角形的三边 $ a $,$ b $,$ c $ 满足 $ c > a > b $,分别以 $ a $,$ b $,$ c $ 为边作三个正方形,把两个较小的正方形放置在最大正方形内,如图,设三个正方形无重叠部分的面积为 $ S_{1} $,均重叠部分的面积为 $ S_{2} $,试判断 $ S_{1} $ 与 $ S_{2} $ 的大小关系。

答案:
14.解因为直角三角形的三边a,b,c满足c>a>b,所以该直角三角形的斜边为c,所以c²=a²+b²,所以c² - a² - b²=0,所以S₁=c² - a² - b²+b(a+b - c)=ab+b² - bc。因为S₂=b(a+b - c)=ab+b² - bc,所以S₁=S₂。
15. (10 分)已知 $ a = 2n $,$ b = n^{2} - 1 $,$ c = n^{2} + 1 $。
(1)当 $ n = 2 $ 时,则以 $ a $,$ b $,$ c $ 为三边长的三角形的面积为
(2)小安猜想:当 $ n $ 取大于 1 的整数时,$ a $,$ b $,$ c $ 为勾股数。你认为小安的猜想正确吗?请说明理由。
(1)当 $ n = 2 $ 时,则以 $ a $,$ b $,$ c $ 为三边长的三角形的面积为
6
;(2)小安猜想:当 $ n $ 取大于 1 的整数时,$ a $,$ b $,$ c $ 为勾股数。你认为小安的猜想正确吗?请说明理由。
答案:
15.解
(1)当n=2时,a=2n=4,b=n² - 1=3,c=n²+1=5,因为3²+4²=5²,所以以a,b,c为三边长的三角形是直角三角形,面积为$\frac{1}{2}$×3×4=6。故答案为6。
(2)小安的猜想正确。理由:a²+b²=(2n)²+(n² - 1)²=4n²+n⁴ - 2n²+1=n⁴+2n²+1=(n²+1)²,c²=(n²+1)²,所以a²+b²=c²,所以当n取大于1的整数时,a,b,c为勾股数,所以小安的猜想正确。
(1)当n=2时,a=2n=4,b=n² - 1=3,c=n²+1=5,因为3²+4²=5²,所以以a,b,c为三边长的三角形是直角三角形,面积为$\frac{1}{2}$×3×4=6。故答案为6。
(2)小安的猜想正确。理由:a²+b²=(2n)²+(n² - 1)²=4n²+n⁴ - 2n²+1=n⁴+2n²+1=(n²+1)²,c²=(n²+1)²,所以a²+b²=c²,所以当n取大于1的整数时,a,b,c为勾股数,所以小安的猜想正确。
查看更多完整答案,请扫码查看


