1. 实数$-\frac{1}{3}$,$0$,$\sqrt{5}$,$1.732$中无理数是(
A.$-\frac{1}{3}$
B.$0$
C.$\sqrt{5}$
D.$1.732$
C
)。A.$-\frac{1}{3}$
B.$0$
C.$\sqrt{5}$
D.$1.732$
答案:
1.C
2. 下面各式中,是最简二次根式的是(
A.$\sqrt{\frac{1}{3}}$
B.$\sqrt{0.5}$
C.$\sqrt{2}$
D.$\sqrt{45}$
C
)。A.$\sqrt{\frac{1}{3}}$
B.$\sqrt{0.5}$
C.$\sqrt{2}$
D.$\sqrt{45}$
答案:
2.C
3. 利用计算器求$\sqrt{9}$的值,依次按键后,则计算器面板显示的结果为(
A.$-3$
B.$3$
C.$\pm 3$
D.$4$
B
)。A.$-3$
B.$3$
C.$\pm 3$
D.$4$
答案:
3.B
4. 下列说法正确的是(
A.$6$是$36$的算术平方根,即$\sqrt{36}=\pm 6$
B.$6$是$(-6)^{2}$的算术平方根,即$\sqrt{(-6)^{2}}=6$
C.$\pm 7$是$49$的平方根,即$\pm \sqrt{49}=7$
D.$\pm 2$是$4$的平方根,即$\sqrt{4}=\pm 2$
B
)。A.$6$是$36$的算术平方根,即$\sqrt{36}=\pm 6$
B.$6$是$(-6)^{2}$的算术平方根,即$\sqrt{(-6)^{2}}=6$
C.$\pm 7$是$49$的平方根,即$\pm \sqrt{49}=7$
D.$\pm 2$是$4$的平方根,即$\sqrt{4}=\pm 2$
答案:
4.B
5. 完全相同的$4$个正方形面积之和是$100$,则正方形的边长是(
A.$2$
B.$5$
C.$10$
D.$20$
B
)。A.$2$
B.$5$
C.$10$
D.$20$
答案:
5.B
6. 下列运算正确的是(
A.$\sqrt{3}+\sqrt{7}=\sqrt{10}$
B.$\sqrt{(-6)^{2}}=-6$
C.$(3-\sqrt{2})^{2}=11-6\sqrt{2}$
D.$6÷ \frac{2}{\sqrt{3}}× \sqrt{3}=3$
C
)。A.$\sqrt{3}+\sqrt{7}=\sqrt{10}$
B.$\sqrt{(-6)^{2}}=-6$
C.$(3-\sqrt{2})^{2}=11-6\sqrt{2}$
D.$6÷ \frac{2}{\sqrt{3}}× \sqrt{3}=3$
答案:
6.C
7. 若$\sqrt{2}$的整数部分用$a$表示,小数部分用$b$表示,则$a + b$的值为(
A.$\sqrt{2}$
B.$\sqrt{2}+1$
C.$2$
D.$\sqrt{2}-1$
A
)。A.$\sqrt{2}$
B.$\sqrt{2}+1$
C.$2$
D.$\sqrt{2}-1$
答案:
7.A
8. 将一组数$\sqrt{2}$,$2$,$\sqrt{6}$,$2\sqrt{2}$,$\sqrt{10}$,$2\sqrt{3}$,$\cdots$,$\sqrt{2n}$,$\cdots$,按以下方式进行排列:
| 第一行 | $\sqrt{2}$ |
| ---- | ---- |
| 第二行 | $2$ $\sqrt{6}$ |
| 第三行 | $2\sqrt{2}$ $\sqrt{10}$ $2\sqrt{3}$ |
| $\cdots\cdots$ | |
则第八行左起第$1$个数是(
A.$7\sqrt{2}$
B.$8\sqrt{2}$
C.$\sqrt{58}$
D.$4\sqrt{7}$
| 第一行 | $\sqrt{2}$ |
| ---- | ---- |
| 第二行 | $2$ $\sqrt{6}$ |
| 第三行 | $2\sqrt{2}$ $\sqrt{10}$ $2\sqrt{3}$ |
| $\cdots\cdots$ | |
则第八行左起第$1$个数是(
C
)。A.$7\sqrt{2}$
B.$8\sqrt{2}$
C.$\sqrt{58}$
D.$4\sqrt{7}$
答案:
8.C
9. 如图,$A$,$B$,$C$均为正方形,若$A$的面积为$10$,$C$的面积为$1$,则$B$的边长可以是
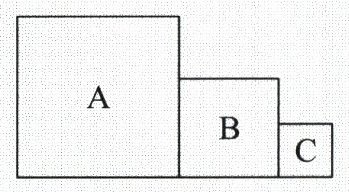
3
。(写出一个答案即可)
答案:
9.2(答案不唯一)
查看更多完整答案,请扫码查看


