《2025年家庭作业八年级数学上册北师大版》

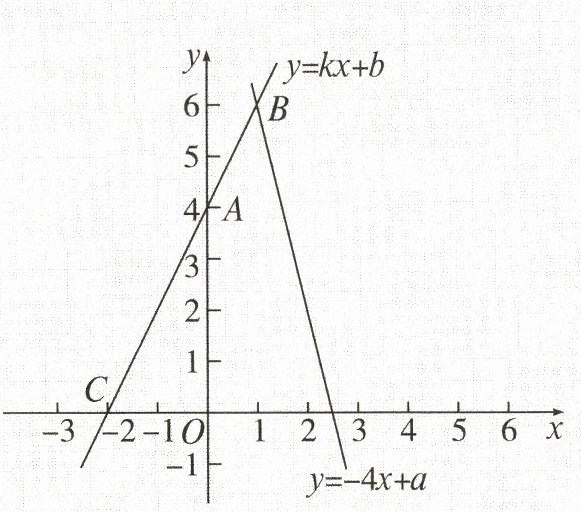
16. (12 分)如图，已知点$A(0,4)$，$C(-2,0)$在直线$l$：$y = kx + b$上，直线$l$和一次函数$y = -4x + a$的图象交于点$B$。
（1）求直线$l$对应的函数表达式；
（2）若点$B$的横坐标是 1，求点$B$的坐标，并直接写出关于$x$，$y$的方程组$\begin{cases}y = kx + b, \\ y = -4x + a\end{cases}$的解；
（3）在（2）的条件下，若点$A$关于$x$轴的对称点为$P$，求$\triangle BPC$的面积。

答案： 16.解
(1)因为点$A(0,4),C(-2,0)$在直线$l:y = kx + b$上，所以$\begin{cases}b = 4,\\-2k + b = 0,\end{cases}$解得$\begin{cases}k = 2,\\b = 4.\end{cases}$
所以直线$l$对应的函数表达式为$y = 2x + 4$。
(2)因为点$B$在直线$l$上，所以当$x = 1$时，$y = 2 + 4 = 6$，所以点$B$的坐标为$(1,6)$。所以关于$x,y$的方程组$\begin{cases}y = kx + b,\\y = -4x + a\end{cases}$的解为$\begin{cases}x = 1,\\y = 6.\end{cases}$
(3)因为点$A$与点$P$关于$x$轴对称，所以点$P(0,-4)$，所以$AP = 4 + 4 = 8$，所以$S_{\triangle BPC} = S_{\triangle PAB} + S_{\triangle PAC} = \frac{1}{2} × 8 × 1 + \frac{1}{2} × 8 × 2 = 12$。

17. (12 分)某地生产一种绿色蔬菜，若在市场上直接销售，每吨利润为 1000 元；经粗加工后销售，每吨利润可达 4500 元；经精加工后销售，每吨利润涨至 7500 元。当地一家农工商会公司收获这种蔬菜 140 吨，该公司加工厂的生产能力是：如果对蔬菜进行粗加工，那么每天可加工 16 吨；如果进行精加工，那么每天可加工 6 吨。但两种加工方式不能同时进行。受季节条件的限制，公司必须在 15 天之内将这批蔬菜全部销售或加工完毕，为此公司研制了三种加工方案。
方案一：将蔬菜全部进行粗加工；
方案二：尽可能多地对蔬菜进行精加工，没有来得及进行加工的蔬菜，在市场上直接销售；
方案三：将部分蔬菜进行精加工，其余蔬菜进行粗加工，并恰好 15 天完成。
你认为选择哪种方案获利最多？为什么？

答案： 17.解方案一：获利$4500 × 140 = 630000$(元)；
方案二：获利$7500 × (6 × 15) + 1000 × (140 - 6 × 15) = 725000$(元)；
方案三：设将$x$吨蔬菜进行精加工，$y$吨蔬菜进行粗加工，根据题意，得$\begin{cases}x + y = 140,\frac{x}{6} + \frac{y}{16} = 15,\end{cases}$解得$\begin{cases}x = 60,\\y = 80.\end{cases}$
获利$7500 × 60 + 4500 × 80 = 810000$(元)。
因为$630000 ＜ 725000 ＜ 810000$，
所以方案三获利最多。