《2025年家庭作业八年级数学上册北师大版》

16. （12 分）如图，在正方形网格中，直线 $l$ 与网格线重合，点 $A$，$C$，$A'$，$B'$ 均在网格的格点上。
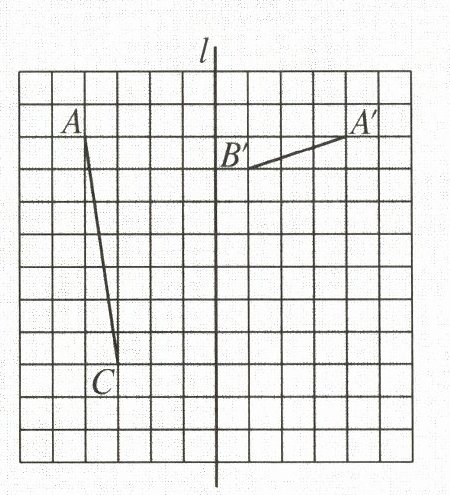
(1) 已知 $\triangle ABC$ 和 $\triangle A'B'C'$ 关于直线 $l$ 对称。
① 请在图中把 $\triangle ABC$ 和 $\triangle A'B'C'$ 补充完整；
② 在以直线 $l$ 为纵轴的平面直角坐标系中，若点 $A$ 的坐标为 $(a,-2b)$，则点 $A'$ 的坐标为(- a, - 2b)。
(2) 已知网格中每个小正方形的边长都为 1，求 $\triangle ABC$ 的面积。

答案：
16.解
(1)①如图，△ABC和△A′B′C′即为所求。

②
∵点A的坐标为(a, - 2b)，点A与点A′关于纵轴对称，
∴点A′的坐标为(- a, - 2b)。故答案为(- a, - 2b)。
(2)S△ABC = 3×7 - $\frac{1}{2}$×3×1 - $\frac{1}{2}$×7×1 - $\frac{1}{2}$×2×6 = 10。

17. （12 分）如图，在平面直角坐标系中，一次函数 $y = -\frac{1}{2}x - 3$ 的图象与 $x$ 轴、$y$ 轴分别交于点 $A$ 和点 $C$，直线 $y = x + b$（$b$ 是常数）与 $x$ 轴交于点 $B$ 且经过点 $C$。
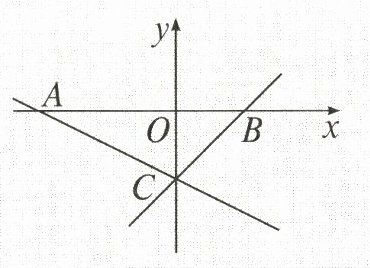
(1) $b =$- 3$$，$AB =$9$$；
(2) 若直线 $DE // y$ 轴且在 $y$ 轴右侧，直线 $DE$ 与直线 $AC$，$BC$ 分别交于点 $D$ 和点 $E$，$DE = 3$，求点 $D$ 的坐标；
(3) 若点 $P$ 是直线 $AC$ 上一点，是否存在点 $P$ 使得 $\triangle ABP$ 的面积为 9？若存在，求出点 $P$ 的坐标；若不存在，说明理由。

答案： 17.解
(1)将x = 0代入y = - $\frac{1}{2}$x - 3，得y = - 3，
所以点C的坐标为(0, - 3)。将点C的坐标代入y = x + b，得b = - 3，则y = x - 3。令y = 0，得x = 3，所以点B的坐标为(3,0)。将y = 0代入y = - $\frac{1}{2}$x - 3，得0 = - $\frac{1}{2}$x - 3，解得x = - 6，所以点A的坐标为(- 6,0)，所以AB = 3 - (- 6) = 9。故答案为 - 3,9。
(2)设点D的横坐标为m，
由DE//y轴知，点E的横坐标为m。
因为直线DE与直线AC，BC分别交于点D和点E，所以D(m, - $\frac{1}{2}$m - 3)，E(m,m - 3)。
由DE = 3得，m - 3 - (- $\frac{1}{2}$m - 3) = 3，解得m = 2，
所以 - $\frac{1}{2}$m - 3 = - $\frac{1}{2}$×2 - 3 = - 4，
故点D的坐标为(2, - 4)。
(3)存在。
设点P的坐标为(x_P,y_P)。因为△ABP的面积为9，所以$\frac{1}{2}$·AB·|y_P| = 9，则y_P = ±2。当y_P = 2时，x_P = - 10；当y_P = - 2时，x_P = - 2。所以点P的坐标为(- 10,2)或(- 2, - 2)。