8. 按一定规律排列的单项式:$a$,$\sqrt{2}a^2$,$\sqrt{3}a^3$,$\sqrt{4}a^4$,$\sqrt{5}a^5$,…,第 $n$ 个单项式是(
A.$\sqrt{n}$
B.$\sqrt{n - 1}a^{n - 1}$
C.$\sqrt{n}a^n$
D.$\sqrt{n}a^{n - 1}$
C
)。A.$\sqrt{n}$
B.$\sqrt{n - 1}a^{n - 1}$
C.$\sqrt{n}a^n$
D.$\sqrt{n}a^{n - 1}$
答案:
8.C
9. 已知直线 $y = kx + b$($k$,$b$ 是常数,$k \neq 0$)经过点 $(1,1)$,且 $y$ 的值随 $x$ 值的增大而减小,则 $b$ 的值可以是
2
。(写出一个即可)
答案:
9.2(答案不唯一)
10. 规定用符号 $[m]$ 表示一个实数 $m$ 的整数部分,例如:$[\frac{2}{3}] = 0$,$[3.14] = 3$,则 $[7 - \sqrt{5}]$ 的值为
4
。
答案:
10.4
11. 如图,在 $2 × 3$ 的网格中,$\angle 1 + \angle 2$ 的度数是
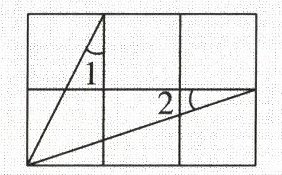
45°
。
答案:
11.45°
12. 已知 $a$,$b$ 均为实数,$a$ 的平方根分别是 $2x - 5$ 与 $x - 7$,$b$ 是 27 的立方根,则 $a - 2b$ 的算术平方根为
$\sqrt{3}$
。
答案:
12.$\sqrt{3}$
13. (8 分)计算:
(1) $(3\sqrt{3} - 1)(3\sqrt{3} + 1) - (2\sqrt{3} - 1)^2$;
(2) $(2\sqrt{12} - \sqrt{\frac{1}{3}}) × \sqrt{6} - \frac{\sqrt{27} + \sqrt{12}}{\sqrt{3}}$。
(1) $(3\sqrt{3} - 1)(3\sqrt{3} + 1) - (2\sqrt{3} - 1)^2$;
(2) $(2\sqrt{12} - \sqrt{\frac{1}{3}}) × \sqrt{6} - \frac{\sqrt{27} + \sqrt{12}}{\sqrt{3}}$。
答案:
13.解
(1)(3$\sqrt{3}$ - 1)(3$\sqrt{3}$ + 1) - (2$\sqrt{3}$ - 1)² =
(3$\sqrt{3}$)² - 1 - (12 - 4$\sqrt{3}$ + 1) = 27 - 1 - 12 + 4$\sqrt{3}$ - 1 =
13 + 4$\sqrt{3}$;
(2)(2$\sqrt{12}$ - $\sqrt{\frac{1}{3}}$)×$\sqrt{6}$ - $\frac{\sqrt{27} + \sqrt{12}}{\sqrt{3}}$ = 2$\sqrt{12}$×$\sqrt{6}$ - $\sqrt{\frac{1}{3}}$×$\sqrt{6}$ - $\sqrt{27}$÷$\sqrt{3}$ - $\sqrt{12}$÷$\sqrt{3}$ = 12$\sqrt{2}$ - $\sqrt{2}$ - 3 - 2 = 11$\sqrt{2}$ - 5。
(1)(3$\sqrt{3}$ - 1)(3$\sqrt{3}$ + 1) - (2$\sqrt{3}$ - 1)² =
(3$\sqrt{3}$)² - 1 - (12 - 4$\sqrt{3}$ + 1) = 27 - 1 - 12 + 4$\sqrt{3}$ - 1 =
13 + 4$\sqrt{3}$;
(2)(2$\sqrt{12}$ - $\sqrt{\frac{1}{3}}$)×$\sqrt{6}$ - $\frac{\sqrt{27} + \sqrt{12}}{\sqrt{3}}$ = 2$\sqrt{12}$×$\sqrt{6}$ - $\sqrt{\frac{1}{3}}$×$\sqrt{6}$ - $\sqrt{27}$÷$\sqrt{3}$ - $\sqrt{12}$÷$\sqrt{3}$ = 12$\sqrt{2}$ - $\sqrt{2}$ - 3 - 2 = 11$\sqrt{2}$ - 5。
查看更多完整答案,请扫码查看


