《2025年顶尖课课练六年级数学上册人教版贵州专版》

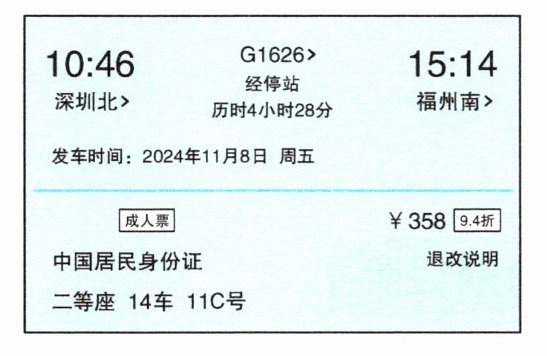
(1) 张叔叔要去福州出差,购票信息如右下图。由于临时有事,张叔叔 $11$ 月 $7$ 日 $16:00$ 接到取消出差的通知,他立即在手机 $APP$ 中进行了退票。按照规定,退票需要扣除相应的手续费,具体退票费用如左下表所示。张叔叔最终收到的退票款是多少钱？

答案： 解：
首先计算退票时间距发车时间：
11月7日16：00到11月8日10：46，11月7日16：00到11月7日24：00，经过的时间是$24 - 16=8$（小时）；11月8日0：00到11月8日10：46，经过了10小时46分。总共经过$8$小时$ + 10$小时$46$分$ = 18$小时$46$分，$18$小时$46$分$＜ 24$小时。
已知车票价格是$358$元，根据退票规定，退票时间$＜ 24$小时，退票费为$20\%$。
那么退票款为$358×(1 - 20\%)$
$=358×0.8$
$ = 286.4$（元）
答：张叔叔最终收到的退票款是$286.4$元。

(2) 新题型 电脑城出售一款标价 $3200$ 元的电脑,从 $10$ 月 $1$ 日开始,价格降低了 $10\%$,$12$ 月 $12$ 日开始又降价 $10\%$。
① 李老师购入这款电脑时价格比原价少 $320$ 元,她是在哪个时间段购入的？
$10$ 月 $1$ 日前 $□$ $10$ 月 $1$ 日$-12$ 月 $11$ 日 $\boxed{\surd}$ $12$ 月 $12$ 日后 $□$
作出判断后在上方相应的 $□$ 里画“$\surd$”,并结合算式说明理由。

② 如果刘老师在 $12$ 月 $13$ 日购买这款电脑,他需要付多少钱？
① 理由：原价3200元，比原价少320元，即现价为$3200 - 320 = 2880$元。10月1日开始第一次降价10%，价格为$3200×(1 - 10\%) = 3200×0.9 = 2880$元。故此时段为10月1日-12月11日。② $3200×(1 - 10\%)×(1 - 10\%) = 3200×0.9×0.9 = 2592$元。答：2592元。

答案： ① 10月1日-12月11日 $\boxed{\surd}$
理由：
原价3200元，比原价少320元，即现价为$3200 - 320 = 2880$元。
10月1日开始第一次降价10%，价格为$3200×(1 - 10\%) = 3200×0.9 = 2880$元。
故此时段为10月1日-12月11日。
② $3200×(1 - 10\%)×(1 - 10\%) = 3200×0.9×0.9 = 2592$元。
答：2592元。

(3) 坚持阅读是一种良好的习惯。宁宁利用周末看一本地理知识书,已看页数与未看页数的比是 $1:5$。如果再看 $40$ 页,那么已看页数就占总页数的 $50\%$。这本书一共有多少页？

答案： 设这本书一共有$x$页。
已看页数与未看页数比是$1:5$，则已看页数占总页数的$\frac{1}{1+5}=\frac{1}{6}$，即$\frac{1}{6}x$页。
再看40页后，已看页数为$\frac{1}{6}x + 40$，此时占总页数的50%，可列方程：
$\frac{1}{6}x + 40 = 50\%x$
$\frac{1}{6}x + 40 = \frac{1}{2}x$
$\frac{1}{2}x - \frac{1}{6}x = 40$
$\frac{3}{6}x - \frac{1}{6}x = 40$
$\frac{2}{6}x = 40$
$\frac{1}{3}x = 40$
$x = 40 ÷ \frac{1}{3}$
$x = 120$
答：这本书一共有120页。

(4) 某小学组织六年级学生一起外出参加研学活动。研学活动共分为两个环节,第一环节的时间占总时间的 $\frac{1}{3}$。如果从第二环节中抽出 $2.5$ 小时给第一环节,那么第二环节的时间占总时间的 $25\%$。本次研学活动的总时间是多少小时？

答案： 设本次研学活动的总时间是 $x$ 小时。
原第一环节的时间为 $\frac{1}{3}x$ 小时，
原第二环节的时间为 $\frac{2}{3}x$ 小时。
根据题意，从第二环节中抽出 $2.5$ 小时给第一环节后，
第一环节的时间变为 $\frac{1}{3}x + 2.5$ 小时，
第二环节的时间变为 $\frac{2}{3}x - 2.5$ 小时。
此时，第二环节的时间占总时间的 $25\%$，即：
$\frac{2}{3}x - 2.5 = 0.25x$
解这个方程，得到：
$\frac{2}{3}x - 0.25x = 2.5$
$\frac{8}{12}x - \frac{3}{12}x = 2.5$
$\frac{5}{12}x = 2.5$
$x = 6$
答：本次研学活动的总时间是 $6$ 小时。