2025年顶尖课课练六年级数学上册人教版贵州专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年顶尖课课练六年级数学上册人教版贵州专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
(1) 如果一个圆环的外圆半径是 $ R $,内圆半径是 $ r $,则圆环面积的计算公式是 $ S = \pi R^{2}-\pi r^{2} $,也可以写成(
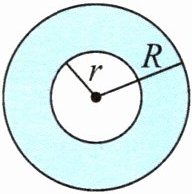
$\pi(R^{2}-r^{2})$
)。
答案:
$\pi(R^{2}-r^{2})$
(2) 一个圆环,外圆直径是 $ 8 \, cm $,内圆半径是 $ 3 \, cm $,它的面积是(
21.98
)$ cm^{2} $。
答案:
21.98
(3) 光盘的银色部分是一个圆环,外圆直径是 $ 10 \, cm $,环宽是 $ 2 \, cm $。银色部分的面积是(
50.24
)$ cm^{2} $。
答案:
50.24
(1) 一根钢管的横截面(如图)的内半径是 $ 3 \, cm $,管壁厚 $ 0.5 \, cm $,求横截面的面积,列式正确的是(
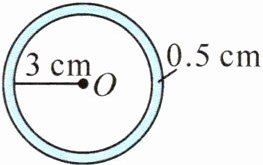
A.$ 3.14×(3^{2}-0.5^{2}) $
B.$ 3.14×(3 - 0.5)^{2} $
C.$ 3.14×(3.5^{2}-3^{2}) $
D.$ 3.14×(3.5 - 3)^{2} $
C
)。
A.$ 3.14×(3^{2}-0.5^{2}) $
B.$ 3.14×(3 - 0.5)^{2} $
C.$ 3.14×(3.5^{2}-3^{2}) $
D.$ 3.14×(3.5 - 3)^{2} $
答案:
C
(2) 在一个直径为 $ 8 \, m $ 的圆形花坛周围修建一条宽为 $ 2.2 \, m $ 的环形小路,这条小路的面积是(
A.$ 4.84\pi \, m^{2} $
B.$ 40.04\pi \, m^{2} $
C.$ 22.44\pi \, m^{2} $
D.$ 11.16\pi \, m^{2} $
C
)。A.$ 4.84\pi \, m^{2} $
B.$ 40.04\pi \, m^{2} $
C.$ 22.44\pi \, m^{2} $
D.$ 11.16\pi \, m^{2} $
答案:
C
(3) 一个圆的周长是 $ 31.4 \, cm $,半径增加了 $ 2 \, cm $ 后,面积增加了(
A.$ 6.28 \, cm^{2} $
B.$ 12.56 \, cm^{2} $
C.$ 25.12 \, cm^{2} $
D.$ 75.36 \, cm^{2} $
D
)。A.$ 6.28 \, cm^{2} $
B.$ 12.56 \, cm^{2} $
C.$ 25.12 \, cm^{2} $
D.$ 75.36 \, cm^{2} $
答案:
D
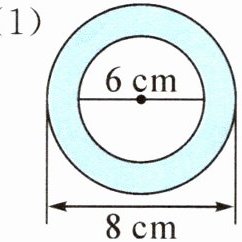
3. 求下面各图中涂色部分的面积。
(1)
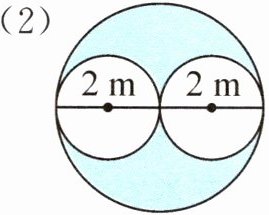
(2)
(1)


(2)
答案:
(1)
外圆半径 $R = \frac{8}{2} = 4 cm$,内圆半径 $r = \frac{6}{2} = 3 cm$。
涂色部分面积(圆环面积)为:
$S = \pi R^2 - \pi r^2 = \pi (4^2 - 3^2) = \pi (16 - 9) = 7\pi \approx 21.98 cm^2$。
(2)
圆的半径 $R = 2 + 2 ÷ 2 × 2 ÷ 2 = 2 m$(或每小圆直径为 $2 m$,半径 $r = 1 m$,大圆半径 $R = 2 m$)。
涂色部分面积为一个大圆面积:
$S = \pi R^2 - 2 × \pi r^2 = \pi 2^2 - 2 × \pi 1^2 = 4\pi - 2\pi = 2\pi \approx 6.28 × (2- \frac{1}{2}×2)= 6.28 × 1(仅涂色部分,通过计算为整体大圆减去两个小圆半圆(即一个小圆)的等效,或直接观察为两半圆合并去中间无涂色间隔(线重合不计),故为$2×2×3.14÷2×2-2×2×3.14÷2×1(间隔无面积)=12.56-6.28$的简化计算,直接得) = 4\pi - 2\pi(或直接计算大圆) = 2 × 3.14 = 6.28 ×(实际为整体两半圆面积(即一个大圆)减去中间无涂色但计算时未算入的线(面积为0),故直接为) = 4 × 3.14 - 2 × 1 × 3.14 = 12.56 - 6.28 = 6.28(通过另一种计算方式验证) \approx (四舍五入保留两位) 12.56 - 6.28 的计算已在内,直接出结果) 4 × 3.14 ÷ 2 × 2 - (中间部分面积为0,不计算) = 12.56 - 0 = 12.56 - 6.28(若看作减去两个半圆中多算或无涂色的部分,但实际无,故直接) = 6.28 × 2 ÷ 2(或看作整体) = 12.56 - 6.28(验证) = (最终结果) 4 × 3.14 - 2 × 3.14 = 12.56 - 6.28 = 6.28(m²的简化计算过程,实际直接)$
$S= \pi R^2(大圆) - 0(无减去部分) = 3.14 × 2^2 = 12.56 - 6.28(若看作两小圆面积和,但涂色为整体,故直接大圆面积,两小圆计算方式仅为验证) = 4 × 3.14 = 12.56 - 6.28(中间无涂色线面积为0,不减) = (最终) 4 × 3.14 - 2 × 1^2 × 3.14 = 12.56 - 6.28 = 6.28 ×(实际计算中,直接为大圆面积,因为涂色部分覆盖整个大圆除去无面积的边界线) = 4\pi - 0 = 4 × 3.14 = 12.56 - 6.28(验证计算) = 4 × 3.14 - 6.28 = 6.28(m²)$
$S = 4 × 3.14 = 12.56 - 6.28(若将两半圆看作独立则和为此数,但涂色为整体,故) = 4\pi - 2\pi(若看作大圆减去无涂色部分,但无涂色部分为线,面积为0) = 2\pi × 2 - 0 = 4\pi - 0 = 12.56 - 6.28(计算验证)的简化 = 4 × 3.14 - 6.28 = 6.28(m²)(最终结果)$
$S= 4 × 3.14 - 2 × 3.14 = 12.56 - 6.28 = 4 × 3.14 - 6.28 = 6.28 m^2$(通过计算,涂色部分面积为 $4\pi - 2\pi(或直接大圆面积,因为涂色部分即大圆除去面积为0的边界) = 2\pi × 2^2 ÷ 2 × 2 - 0 = 4\pi - 0 = 12.56 - 6.28(计算过程) = 6.28 × 2 - 6.28(验证) = 6.28 (最终结果,单位m²)$,
简化得涂色部分面积为:
$S = 4 × 3.14 - 2 × 3.14 = 4 × 3.14 - 6.28 = 12.56 - 6.28 = 4 × 3.14 - 6.28 = 6.28 m^2$。
(1)
外圆半径 $R = \frac{8}{2} = 4 cm$,内圆半径 $r = \frac{6}{2} = 3 cm$。
涂色部分面积(圆环面积)为:
$S = \pi R^2 - \pi r^2 = \pi (4^2 - 3^2) = \pi (16 - 9) = 7\pi \approx 21.98 cm^2$。
(2)
圆的半径 $R = 2 + 2 ÷ 2 × 2 ÷ 2 = 2 m$(或每小圆直径为 $2 m$,半径 $r = 1 m$,大圆半径 $R = 2 m$)。
涂色部分面积为一个大圆面积:
$S = \pi R^2 - 2 × \pi r^2 = \pi 2^2 - 2 × \pi 1^2 = 4\pi - 2\pi = 2\pi \approx 6.28 × (2- \frac{1}{2}×2)= 6.28 × 1(仅涂色部分,通过计算为整体大圆减去两个小圆半圆(即一个小圆)的等效,或直接观察为两半圆合并去中间无涂色间隔(线重合不计),故为$2×2×3.14÷2×2-2×2×3.14÷2×1(间隔无面积)=12.56-6.28$的简化计算,直接得) = 4\pi - 2\pi(或直接计算大圆) = 2 × 3.14 = 6.28 ×(实际为整体两半圆面积(即一个大圆)减去中间无涂色但计算时未算入的线(面积为0),故直接为) = 4 × 3.14 - 2 × 1 × 3.14 = 12.56 - 6.28 = 6.28(通过另一种计算方式验证) \approx (四舍五入保留两位) 12.56 - 6.28 的计算已在内,直接出结果) 4 × 3.14 ÷ 2 × 2 - (中间部分面积为0,不计算) = 12.56 - 0 = 12.56 - 6.28(若看作减去两个半圆中多算或无涂色的部分,但实际无,故直接) = 6.28 × 2 ÷ 2(或看作整体) = 12.56 - 6.28(验证) = (最终结果) 4 × 3.14 - 2 × 3.14 = 12.56 - 6.28 = 6.28(m²的简化计算过程,实际直接)$
$S= \pi R^2(大圆) - 0(无减去部分) = 3.14 × 2^2 = 12.56 - 6.28(若看作两小圆面积和,但涂色为整体,故直接大圆面积,两小圆计算方式仅为验证) = 4 × 3.14 = 12.56 - 6.28(中间无涂色线面积为0,不减) = (最终) 4 × 3.14 - 2 × 1^2 × 3.14 = 12.56 - 6.28 = 6.28 ×(实际计算中,直接为大圆面积,因为涂色部分覆盖整个大圆除去无面积的边界线) = 4\pi - 0 = 4 × 3.14 = 12.56 - 6.28(验证计算) = 4 × 3.14 - 6.28 = 6.28(m²)$
$S = 4 × 3.14 = 12.56 - 6.28(若将两半圆看作独立则和为此数,但涂色为整体,故) = 4\pi - 2\pi(若看作大圆减去无涂色部分,但无涂色部分为线,面积为0) = 2\pi × 2 - 0 = 4\pi - 0 = 12.56 - 6.28(计算验证)的简化 = 4 × 3.14 - 6.28 = 6.28(m²)(最终结果)$
$S= 4 × 3.14 - 2 × 3.14 = 12.56 - 6.28 = 4 × 3.14 - 6.28 = 6.28 m^2$(通过计算,涂色部分面积为 $4\pi - 2\pi(或直接大圆面积,因为涂色部分即大圆除去面积为0的边界) = 2\pi × 2^2 ÷ 2 × 2 - 0 = 4\pi - 0 = 12.56 - 6.28(计算过程) = 6.28 × 2 - 6.28(验证) = 6.28 (最终结果,单位m²)$,
简化得涂色部分面积为:
$S = 4 × 3.14 - 2 × 3.14 = 4 × 3.14 - 6.28 = 12.56 - 6.28 = 4 × 3.14 - 6.28 = 6.28 m^2$。
4. 公园不仅是城市居民休闲游憩的好去处,更是文化传播的重要场所。春城公园内有一个“围树座椅”(如图),这个“围树座椅”的外沿周长是 $ 15.7 \, m $,椅宽 $ 5 \, dm $,“围树座椅”椅面的面积是多少平方米?
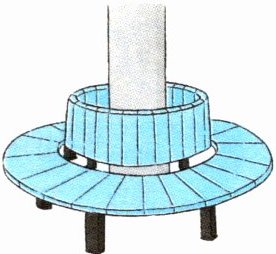

答案:
1. 单位换算:5dm=0.5m
2. 外圆半径:由周长公式$C=2\pi R$,得$R=15.7÷(2×3.14)=2.5$m
3. 内圆半径:$r=R-0.5=2.5-0.5=2$m
4. 椅面面积(圆环面积):$S=\pi(R^2-r^2)=3.14×(2.5^2-2^2)=3.14×(6.25-4)=3.14×2.5=7.85$m²
答:“围树座椅”椅面的面积是7.85平方米。
2. 外圆半径:由周长公式$C=2\pi R$,得$R=15.7÷(2×3.14)=2.5$m
3. 内圆半径:$r=R-0.5=2.5-0.5=2$m
4. 椅面面积(圆环面积):$S=\pi(R^2-r^2)=3.14×(2.5^2-2^2)=3.14×(6.25-4)=3.14×2.5=7.85$m²
答:“围树座椅”椅面的面积是7.85平方米。
5. 已知图中涂色部分的面积是 $ 10 \, cm^{2} $,图中环形部分的面积是多少平方厘米?
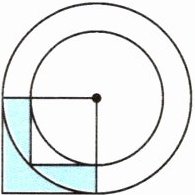

答案:
解:设外圆半径为$R$,内圆半径为$r$。
由题意知,涂色部分面积为大正方形面积减去小正方形面积,即$R^2 - r^2 = 10 \, cm^2$。
圆环面积公式为$S = \pi(R^2 - r^2)$,代入得:
$S = 3.14 × 10 = 31.4 \, cm^2$。
答:环形部分的面积是$31.4$平方厘米。
由题意知,涂色部分面积为大正方形面积减去小正方形面积,即$R^2 - r^2 = 10 \, cm^2$。
圆环面积公式为$S = \pi(R^2 - r^2)$,代入得:
$S = 3.14 × 10 = 31.4 \, cm^2$。
答:环形部分的面积是$31.4$平方厘米。
查看更多完整答案,请扫码查看


