《2025年顶尖课课练六年级数学上册人教版贵州专版》

1. 根据下面的条件,在括号里填上地名。

(1) 趵突泉在老金线泉南偏西 $20^{\circ}$ 方向上。
(2) 漱玉泉在老金线泉西偏北 $20^{\circ}$ 方向上。
(3) 趵突泉在杜康泉的正南方。
(4) 无忧泉在趵突泉的正南方。
(5) 万竹园在趵突泉西偏南 $45^{\circ}$ 方向上。
(6) 白龙湾在万竹园南偏西 $30^{\circ}$ 方向上。

答案： 漱玉泉；杜康泉；老金线泉；万竹园；无忧泉；白龙湾

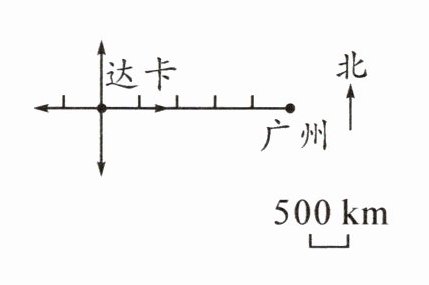
2. 海上丝绸之路是古代我国与外国交通贸易和文化交往的海上通道,广州是其中一个主要港口。广州位于孟加拉国首都达卡的正东方向,距离 $2500$ km。根据下面的描述,在图中标出海上丝绸之路途经的几个城市的位置。
(1) 孟买在达卡的西偏南 $15^{\circ}$ 方向,距离是 $2000$ km。
(2) 科伦坡在达卡的西偏南 $60^{\circ}$ 方向,距离是 $2000$ km。
(3) 马斯喀特在广州的正西方向,距离是 $5500$ km。
(4) 曼谷在达卡的东偏南 $45^{\circ}$ 方向,距离是 $1500$ km。

答案： 1 厘米表示 500 km。
(1) 孟买：$2000 ÷ 500 = 4$（cm），
即孟买在达卡西偏南 $15°$ 方向，距离是 4 cm；
(2) 科伦坡：$2000 ÷ 500 = 4$（cm），
即科伦坡在达卡西偏南 $60°$ 方向，距离是 4 cm；
(3) 马斯喀特：$5500 ÷ 500 = 11$（cm），
广州与达卡相距$2500 ÷ 500 = 5$（cm），
即马斯喀特在广州正西方向，距离是$11 - 5 = 6$（cm）；
(4) 曼谷：$1500 ÷ 500 = 3$（cm），
即曼谷在达卡东偏南 $45°$ 方向，距离是 3 cm。
根据以上数据在图中标出各城市位置即可。

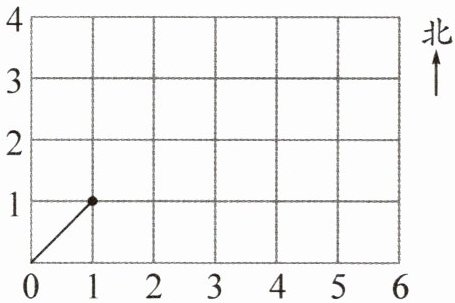
3. 如图,每个小正方形的对角线长 $15$ km。
(1) 一辆小汽车原来的位置是 $(1,1)$,它先向东偏北 $45^{\circ}$ 方向行驶 $45$ km 到达 $(4,4)$,再向东偏南 $45^{\circ}$ 方向行驶 $30$ km 到达 $(6,2)$,最后向南偏西 $45^{\circ}$ 方向行驶 $(30)$km 到达 $(4,0)$。
(2) 若小汽车的行驶速度是每小时 $60$ km,则行驶完上面的路程需要 $(1.75)$小时。

答案：
(1) $(4,4)$；$(6,2)$；$30$
(2) $1.75$

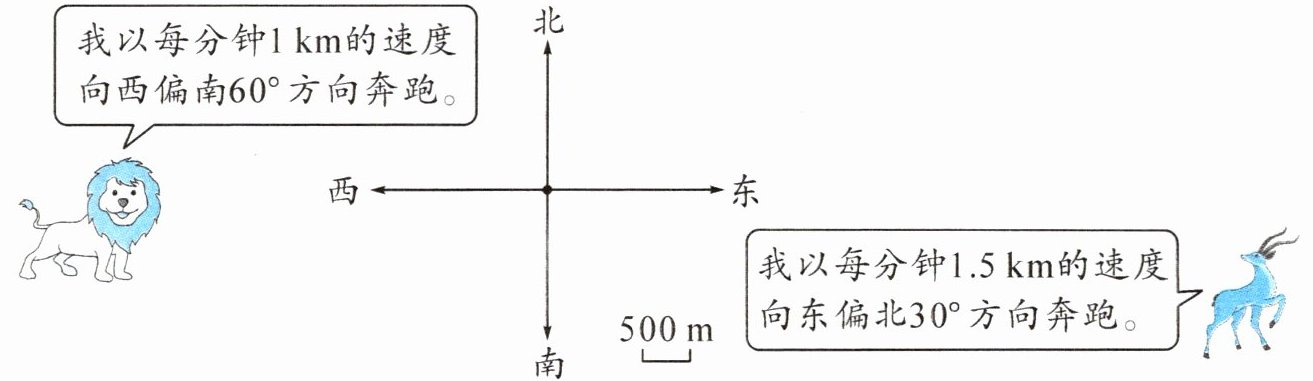
4. 我国自主研发的北斗卫星导航系统日趋成熟。通过卫星定位到非洲草原上一头狮子正要捕获一只羚羊。突然,它们受到了惊吓,请你在图中标出 $2$ 分钟后它们的位置。

答案： 1. 计算狮子2分钟后的位置：
速度为每分钟$1km$，2分钟移动距离为$1×2 = 2km = 2000m$。
方向为西偏南$60^{\circ}$，从原点向西偏南$60^{\circ}$方向量取$2000÷500 = 4$个单位长度，标出狮子2分钟后的位置。
2. 计算羚羊2分钟后的位置：
速度为每分钟$1.5km$，2分钟移动距离为$1.5×2=3km = 3000m$。
方向为东偏北$30^{\circ}$，从原点向东偏北$30^{\circ}$方向量取$3000÷500 = 6$个单位长度，标出羚羊2分钟后的位置。
（在原图上按照上述方法进行标注）。