1 根据下面的信息,寻找合适的量,写出几个关于这些量的比。


答案:
1. 明明年龄与爸爸年龄的比:12:38=6:19
2. 明明年龄与舅舅年龄的比:12:35
3. 爸爸年龄与舅舅年龄的比:38:35
4. 爸爸月工资与舅舅月工资的比:(80000÷12):3600=10000:5400=50:27
5. 爸爸年工资与舅舅年工资的比:80000:(3600×12)=80000:43200=50:27
2. 明明年龄与舅舅年龄的比:12:35
3. 爸爸年龄与舅舅年龄的比:38:35
4. 爸爸月工资与舅舅月工资的比:(80000÷12):3600=10000:5400=50:27
5. 爸爸年工资与舅舅年工资的比:80000:(3600×12)=80000:43200=50:27
2 看图回答下列问题。
(1)大正方形与小正方形的面积比是多少?
(2)大正方形与圆的面积比是多少?
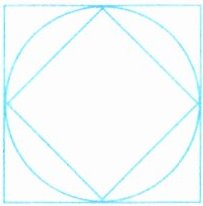
(1)大正方形与小正方形的面积比是多少?
(2)大正方形与圆的面积比是多少?

答案:
(1) 设圆的半径为$r$,则大正方形的边长为$2r$,大正方形的面积为$S_{大正方形}=(2r)^2 = 4r^2$。
小正方形的对角线长等于圆的直径$2r$,根据小正方形面积公式$S = \frac{1}{2}× 对角线×对角线$,可得小正方形面积$S_{小正方形}=\frac{1}{2}×2r×2r = 2r^2$。
所以$S_{大正方形}:S_{小正方形}=4r^2:2r^2 = 2:1$。
(2) 圆的面积$S_{圆}=\pi r^2$,大正方形面积$S_{大正方形}=4r^2$,所以$S_{大正方形}:S_{圆}=4r^2:\pi r^2 = 4:\pi$。
综上,答案为:
(1)$2:1$;
(2)$4:\pi$。
(1) 设圆的半径为$r$,则大正方形的边长为$2r$,大正方形的面积为$S_{大正方形}=(2r)^2 = 4r^2$。
小正方形的对角线长等于圆的直径$2r$,根据小正方形面积公式$S = \frac{1}{2}× 对角线×对角线$,可得小正方形面积$S_{小正方形}=\frac{1}{2}×2r×2r = 2r^2$。
所以$S_{大正方形}:S_{小正方形}=4r^2:2r^2 = 2:1$。
(2) 圆的面积$S_{圆}=\pi r^2$,大正方形面积$S_{大正方形}=4r^2$,所以$S_{大正方形}:S_{圆}=4r^2:\pi r^2 = 4:\pi$。
综上,答案为:
(1)$2:1$;
(2)$4:\pi$。
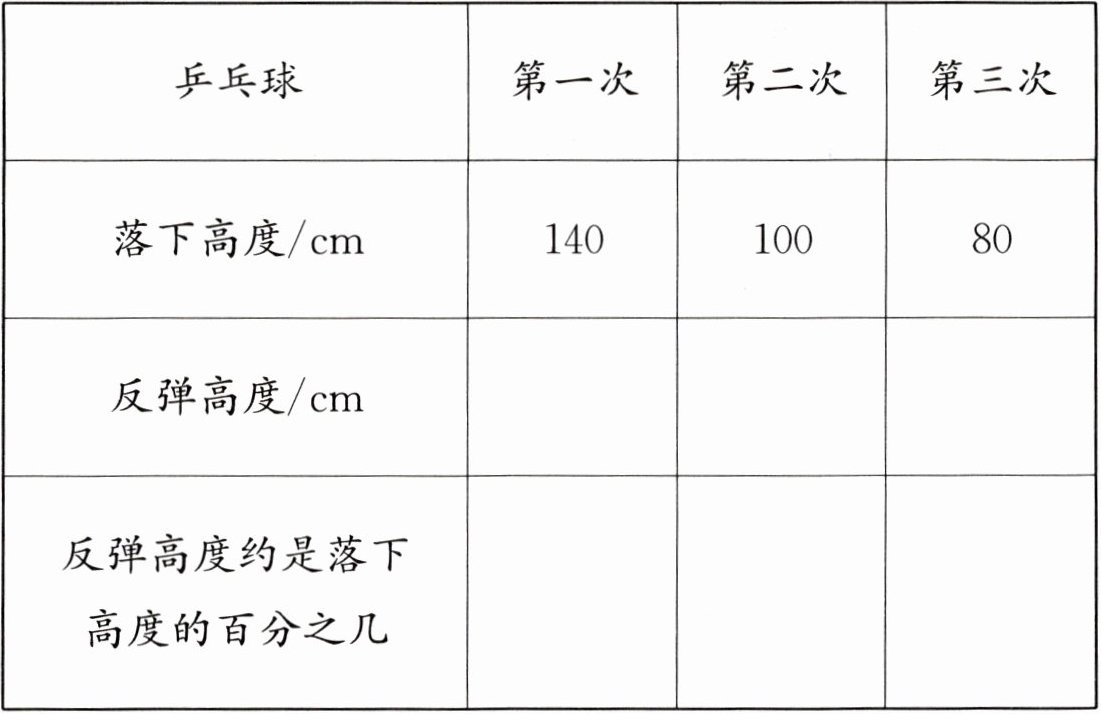
1 将同一个乒乓球从不同的高度自由落下。完成下面的实验,并填空。
|乒乓球|第一次|第二次|第三次|
|落下高度/cm|140|100|80|
|反弹高度/cm|
|反弹高度约是落下高度的百分之几|
乒乓球从不同的高度下落,它的反弹高度是(
|乒乓球|第一次|第二次|第三次|
|落下高度/cm|140|100|80|
|反弹高度/cm|
70
|50
|40
||反弹高度约是落下高度的百分之几|
50%
|50%
|50%
|
乒乓球从不同的高度下落,它的反弹高度是(
不同
)的,但乒乓球的反弹高度与落下高度的百分比大约是(50%
)。
答案:
70;50;40;50%;50%;50%;不同;50%
查看更多完整答案,请扫码查看


