《2025年世纪金榜新视野暑假作业高一数学》

17.(15分)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下.

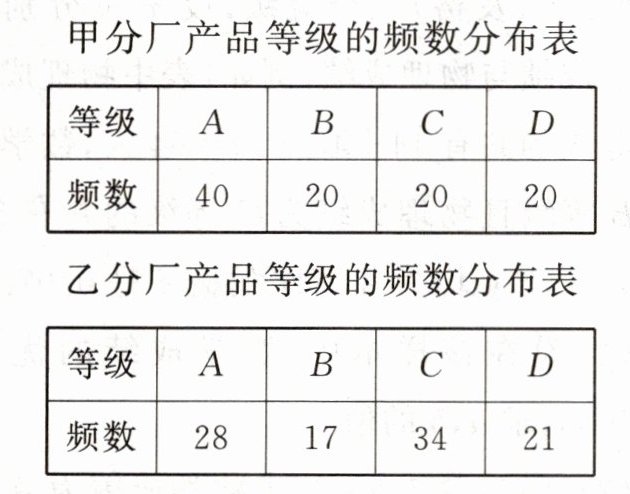
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率.
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?

答案： 【解析】：
本题主要考查概率和平均利润的计算，以及如何通过比较平均利润来做出决策。
对于第一问，我们需要根据频数分布表来估计甲，乙两分厂加工出来的一件产品为A级品的概率。概率的计算公式是“成功的频数”除以“总的试验次数”。
对于第二问，我们需要分别计算甲，乙两分厂加工100件产品的平均利润。平均利润的计算公式是“总利润”除以“产品数量”。其中，总利润是每件产品的利润（加工费减去成本费或者赔偿费）之和。我们需要根据产品的等级和对应的加工费，成本费或者赔偿费来计算每件产品的利润。
最后，我们需要比较甲，乙两分厂的平均利润，选择平均利润更高的分厂来承接加工业务。
【答案】：
(1)根据频数分布表，甲分厂A级品的频数是40，总的试验次数是100，所以甲分厂加工出来的一件产品为A级品的概率是$\frac{40}{100} = 0.4$。同理，乙分厂A级品的频数是28，总的试验次数也是100，所以乙分厂加工出来的一件产品为A级品的概率是$\frac{28}{100} = 0.28$。
(2)甲分厂加工100件产品的总利润是：
$40 × (90 - 25) + 20 × (50 - 25) + 20 × (20 - 25) - 20 × (50 + 25) = 40 × 65 + 20 × 25 + 20 × (-5) - 20 × 75 = 2600 + 500 - 100 - 1500 = 1500 \text{(元]}$
所以甲分厂加工100件产品的平均利润是$\frac{1500}{100} = 15$元/件。
乙分厂加工100件产品的总利润是：
$28 × (90 - 20) + 17 × (50 - 20) + 34 × (20 - 20) - 21 × (50 + 20) = 28 × 70 + 17 × 30 + 34 × 0 - 21 × 70 = 1960 + 510 + 0 - 1470 = 1000 \text{(元]}$
所以乙分厂加工100件产品的平均利润是$\frac{1000}{100} = 10$元/件。
因为$15 ＞ 10$，所以厂家应选择甲分厂承接加工业务。

18.(17分)一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量(单位:辆)如下表.
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值.
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分为:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.

答案：
(1) 设该厂这个月共生产轿车 $ n $ 辆，由分层抽样性质得：
$\frac{10}{n} = \frac{40 + 60}{n} \implies \frac{10}{n} = \frac{100}{n} \quad (\text{此处应为} \frac{10}{50} = \frac{100}{n})$
修正得 $ \frac{10}{50} = \frac{100}{n} \implies n = 500 $。
则 $ z = 500 - (40 + 60 + 30 + 70 + 60) = 240 $。
(2) C类轿车中舒适型与标准型的数量比为 $ 60:240 = 1:4 $，样本容量为5，故抽取舒适型1辆（记为$ a $），标准型4辆（记为$ b_1,b_2,b_3,b_4 $）。
样本总体为$ \{a,b_1,b_2,b_3,b_4\} $，任取2辆的基本事件共10个：
$ (a,b_1),(a,b_2),(a,b_3),(a,b_4),(b_1,b_2),(b_1,b_3),(b_1,b_4),(b_2,b_3),(b_2,b_4),(b_3,b_4) $。
至少有1辆舒适型的事件有4个，故概率为 $ \frac{4}{10} = \frac{2}{5} $。
(3) 样本平均数 $ \bar{x} = \frac{1}{8}(9.4 + 8.6 + 9.2 + 9.6 + 8.7 + 9.3 + 9.0 + 8.2) = 9.0 $。
与样本平均数之差的绝对值不超过0.5的数为：9.4,8.6,9.2,8.7,9.3,9.0（共6个）。
故概率为 $ \frac{6}{8} = \frac{3}{4} $。
答案
(1) $ 240 $
(2) $ \frac{2}{5} $
(3) $ \frac{3}{4} $