《2025年世纪金榜新视野暑假作业高一数学》

16. (15分)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,$AD= 2,AB= 1,$$∠BAD= 60^{\circ }$,平面$PCD⊥$平面ABCD,点M为PC上一点.
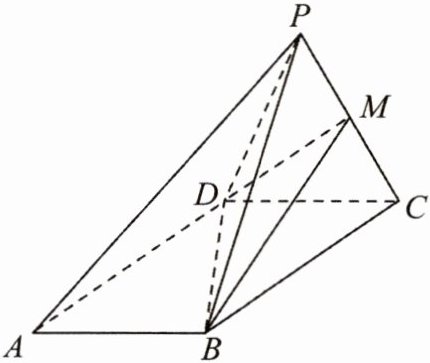
(1)若$PA// $平面MBD,求证:点M为PC中点.
(2)求证:平面$MBD⊥$平面PCD.

答案：
(1)证明：连接AC交BD于点O，连接OM。
∵底面ABCD为平行四边形，
∴O为AC中点。
∵PA//平面MBD，PA⊂平面PAC，平面PAC∩平面MBD=OM，
∴PA//OM。
在△PAC中，O为AC中点，PA//OM，
∴M为PC中点。
(2)证明：在△ABD中，AD=2，AB=1，∠BAD=60°，
由余弦定理得BD²=AB²+AD²-2AB·ADcos60°=1+4-2×1×2×(1/2)=3，
∴BD=√3。
∵AB²+BD²=1+3=4=AD²，
∴AB⊥BD。
∵底面ABCD为平行四边形，
∴AB//CD，
∴CD⊥BD。
∵平面PCD⊥平面ABCD，平面PCD∩平面ABCD=CD，BD⊂平面ABCD，
∴BD⊥平面PCD。
∵BD⊂平面MBD，
∴平面MBD⊥平面PCD。

17. (15分)如图,四棱锥P-ABCD中,$PA⊥$底面ABCD,$AB⊥AD,AB// DC$,E,F分别为PC,DC的中点,$PA= DC= 2AB= 2AD= 2$.
(1)证明:平面$PAD// $平面EBF.
(2)求三棱锥P-BED的体积.

答案： 【解析】：
(1) 平面$PAD$与平面$EBF$的平行关系证明：
第一步，根据题目条件，$E$和$F$分别是$PC$和$DC$的中点。
第二步，根据线段的中点性质，有$EF // PD$。
第三步，由于$EF$在平面$EBF$内，且$PD$在平面$PAD$内，根据平行线与平面的性质，得出$EF //$ 平面$PAD$。
第四步，由于$AB // DC$且$AB = \frac{1}{2}DC$，结合$F$为$DC$的中点，得出$DF // AB$且$DF = AB$。
第五步，根据平行四边形的性质，四边形$ABFD$为平行四边形，所以$AD // BF$。
第六步，由于$BF$在平面$EBF$内，且$AD$在平面$PAD$内，根据平行线与平面的性质，得出$AD //$ 平面$EBF$。
第七步，由于两平面都平行于同一条直线（即$EF$和$AD$），且这两直线相交于一点（即它们不平行），根据平面的平行判定定理，得出平面$PAD //$ 平面$EBF$。
(2) 三棱锥$P-BED$的体积计算：
第一步，根据题目条件，$PA \perp$ 底面$ABCD$，所以$PA$是三棱锥$P-BED$的高。
第二步，计算底面$BED$的面积。由于$AB // DC$且$AB = \frac{1}{2}DC = 1$，$AD = 1$，且$AB \perp AD$，根据直角三角形的面积公式，得出$S_{\triangle ABD} = \frac{1}{2} × AB × AD = \frac{1}{2}$。
第三步，由于$F$是$DC$的中点，且$AB // DC$，所以$S_{\triangle BCD} = 2S_{\triangle ABD} = 1$（因为$DC$是$AB$的两倍，且高相同）。
第四步，由于$E$是$PC$的中点，根据中点性质，$E$到平面$ABCD$的距离是$\frac{1}{2}PA = 1$。但由于我们要求的是三棱锥$P-BED$的体积，所以实际上应该用底面$BDE$（即$\triangle BCD$的一半，因为$F$是$DC$的中点）和高$PA$来计算。因此，$S_{\triangle BDE} = \frac{1}{2}S_{\triangle BCD} = \frac{1}{2}$。
第五步，根据三棱锥的体积公式$V = \frac{1}{3} × \text{底面积} × \text{高}$，得出$V_{P-BED} = \frac{1}{3} × S_{\triangle BDE} × PA = \frac{1}{3} × \frac{1}{2} × 2 = \frac{1}{3}$。
【答案】：
(1) 平面$PAD //$ 平面$EBF$，证明过程见上述解析。
(2) 三棱锥$P-BED$的体积为$\frac{1}{3}$。