《2025年世纪金榜新视野暑假作业高一数学》

12. 过半径为2的球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积为3π.

答案： 【解析】：
本题主要考查球的性质以及圆的面积公式。
首先，根据题意，球的半径为$2$，过球的一条半径的中点作垂直于该半径的平面，所得的截面是一个圆。
需要求出这个圆的半径。
由于截面过球的一条半径的中点，且垂直于该半径，根据勾股定理，截面圆的半径$r$可以通过下面的方式求出：
设球心为$O$，截面圆心为$O'$，球的一条半径为$OP$，$P$为该半径的中点，也是截面圆上的一点。
连接$OO'$和$O'P$，由于$OO'$垂直于截面，所以$OO'$垂直于$O'P$。
根据勾股定理，有：
$r = \sqrt{R^{2} - (\frac{R}{2})^{2}} = \sqrt{2^{2} - 1^{2}} = \sqrt{3}$，
其中，$R$是球的半径，$r$是截面圆的半径。
然后，利用圆的面积公式$S = \pi r^{2}$，可以求出截面圆的面积：
$S = \pi × (\sqrt{3})^{2} = 3\pi$。
【答案】：
$3\pi$。

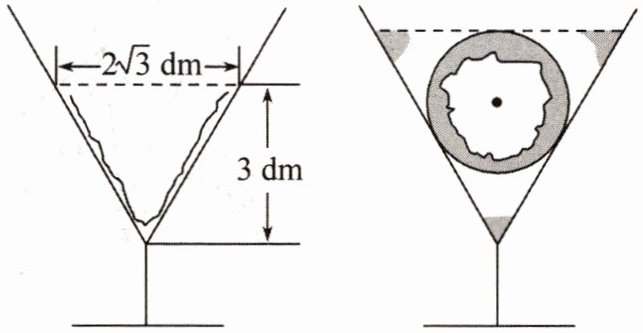
13. 如图,圆锥状容器内盛有水,水深3 dm,水面直径$2\sqrt {3}dm$放人一个铁球后,水恰好把铁球淹没,则该铁球的体积为______$dm^{3}$.

9π

答案： 解：设圆锥容器底面半径为$R$，高为$H$，放入铁球后水面高为$h$，铁球半径为$r$。
由题意，未放入铁球时，水面半径$r_1 = \sqrt{3}\ \text{dm}$，水深$h_1 = 3\ \text{dm}$。根据相似三角形，$\frac{r_1}{h_1} = \frac{R}{H}$，即$\frac{\sqrt{3}}{3} = \frac{R}{H}$，得$R = \frac{\sqrt{3}}{3}H$。
放入铁球后，水恰好淹没铁球，此时水面高为$h = 2r$（球直径等于水面高度），水面半径$r_2 = \frac{\sqrt{3}}{3}h = \frac{2\sqrt{3}}{3}r$。
铁球体积$V_{\text{球}} = \frac{4}{3}\pi r^3$。
未放入铁球时水的体积$V_{\text{水}} = \frac{1}{3}\pi r_1^2 h_1 = \frac{1}{3}\pi (\sqrt{3})^2 × 3 = 3\pi$。
放入铁球后，水和铁球的总体积等于此时圆锥内水的体积：$V_{\text{水}} + V_{\text{球}} = \frac{1}{3}\pi r_2^2 h$。
代入得：$3\pi + \frac{4}{3}\pi r^3 = \frac{1}{3}\pi \left(\frac{2\sqrt{3}}{3}r\right)^2 (2r)$。
化简右边：$\frac{1}{3}\pi × \frac{4 × 3}{9}r^2 × 2r = \frac{8}{9}\pi r^3$。
方程：$3\pi + \frac{4}{3}\pi r^3 = \frac{8}{9}\pi r^3$，两边同除以$\pi$：$3 + \frac{4}{3}r^3 = \frac{8}{9}r^3$。
解得$r^3 = \frac{27}{4}$，则$V_{\text{球}} = \frac{4}{3}\pi r^3 = \frac{4}{3}\pi × \frac{27}{4} = 9\pi$。
答案：$9\pi$

14. 如图,已知四棱锥P-ABCD,底面AB-CD为正方形,$PA⊥$平面ABCD.
给出下列结论:
①$PB⊥AC;$
②平面PAB与平面PCD的交线与AB平行;
③平面$PBD⊥$平面PAC;
④$\triangle PCD$为锐角三角形.其中正确结论的序号是______②③.

答案： 【解析】：
本题可根据线面垂直的性质、面面平行的性质定理以及面面垂直的判定定理来逐一分析各个结论。
判断结论①：$PB⊥AC$是否成立
假设$PB\perp AC$，已知$PA\perp$平面$ABCD$，$AC\subset$平面$ABCD$，则$PA\perp AC$。
若$PB\perp AC$，$PA\cap PB = P$，$PA,PB\subset$平面$PAB$，根据直线与平面垂直的判定定理可知$AC\perp$平面$PAB$，那么$AC\perp AB$，但底面$ABCD$为正方形，$AC$与$AB$的夹角为$45^{\circ}$，并不垂直，所以假设不成立，即$PB$与$AC$不垂直，故①错误。
判断结论②：平面$PAB$与平面$PCD$的交线与$AB$平行是否成立
因为底面$ABCD$为正方形，所以$AB// CD$，又$AB\not\subset$平面$PCD$，$CD\subset$平面$PCD$，根据直线与平面平行的判定定理可知$AB//$平面$PCD$。
由于$AB\subset$平面$PAB$，平面$PAB$与平面$PCD$的交线为$l$，根据面面平行的性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行，可得$AB// l$，故②正确。
判断结论③：平面$PBD⊥$平面$PAC$是否成立
已知$PA\perp$平面$ABCD$，$BD\subset$平面$ABCD$，所以$PA\perp BD$。
因为底面$ABCD$为正方形，所以$AC\perp BD$，又$PA\cap AC = A$，$PA,AC\subset$平面$PAC$，根据直线与平面垂直的判定定理可知$BD\perp$平面$PAC$。
因为$BD\subset$平面$PBD$，根据面面垂直的判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直，可得平面$PBD\perp$平面$PAC$，故③正确。
判断结论④：$\triangle PCD$为锐角三角形是否成立
因为$PA\perp$平面$ABCD$，$CD\subset$平面$ABCD$，所以$PA\perp CD$，又$AD\perp CD$，$PA\cap AD = A$，$PA,AD\subset$平面$PAD$，根据直线与平面垂直的判定定理可知$CD\perp$平面$PAD$，则$CD\perp PD$，即$\angle PDC = 90^{\circ}$，所以$\triangle PCD$是直角三角形，不是锐角三角形，故④错误。
综上，正确结论的序号是②③。
【答案】：②③

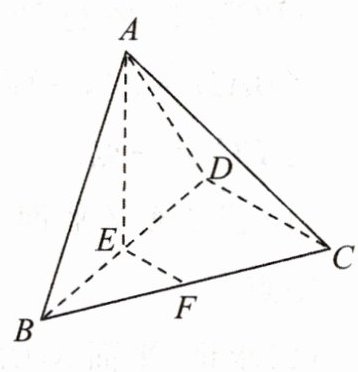
15. (13分)如图,在三棱锥A-BCD中,点E,F分别是BD,BC的中点,$AB= AD,AE⊥BC$.求证:
(1)$EF// $平面ACD.
(2)$AE⊥CD$.

答案： 【解析】：
(1) 本题主要考查线面平行的判定定理，即如果平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。在三棱锥$A - BCD$中，已知点$E$，$F$分别是$BD$，$BC$的中点，根据三角形中位线定理，在$\triangle BCD$中，$EF$是中位线，所以$EF// CD$。又因为$EF$不在平面$ACD$内，$CD$在平面$ACD$内，满足线面平行的判定定理的条件，从而可以证明$EF//$平面$ACD$。
(2) 本题主要考查线面垂直的性质和判定定理。要证明$AE\perp CD$，可先证明$AE$垂直于包含$CD$的平面，即证明$AE$垂直于平面$ACD$中的两条相交直线。已知$AB = AD$，$E$是$BD$中点，根据等腰三角形三线合一的性质，可得$AE\perp BD$。再结合已知$AE\perp BC$，$BD\cap BC = B$，$AE$垂直于平面$BCD$中的两条相交直线，所以$AE\perp$平面$BCD$。因为$CD\subset$平面$BCD$，根据线面垂直的性质，如果一条直线垂直于一个平面，那么该直线与平面内的任意一条直线垂直，所以$AE\perp CD$。
(1)证明：
因为点$E$，$F$分别是$BD$，$BC$的中点，
所以在$\triangle BCD$中，$EF$是中位线，
根据三角形中位线定理可得$EF// CD$。
又因为$EF\not\subset$平面$ACD$，$CD\subset$平面$ACD$，
根据线面平行的判定定理：如果平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行，
所以$EF//$平面$ACD$。
(2)证明：
因为$AB = AD$，$E$是$BD$中点，
根据等腰三角形三线合一的性质，可得$AE\perp BD$。
又因为$AE\perp BC$，$BD\cap BC = B$，$BD\subset$平面$BCD$，$BC\subset$平面$BCD$，
根据线面垂直的判定定理：如果一条直线与一个平面内的两条相交直线都垂直，那么这条直线与这个平面垂直，
所以$AE\perp$平面$BCD$。
因为$CD\subset$平面$BCD$，
根据线面垂直的性质：如果一条直线垂直于一个平面，那么该直线与平面内的任意一条直线垂直，
所以$AE\perp CD$。
【答案】：
(1) 证明：因为点$E$，$F$分别是$BD$，$BC$的中点，所以$EF// CD$。又因为$EF\not\subset$平面$ACD$，$CD\subset$平面$ACD$，所以$EF//$平面$ACD$。
(2) 证明：因为$AB = AD$，$E$是$BD$中点，所以$AE\perp BD$。又因为$AE\perp BC$，$BD\cap BC = B$，$BD\subset$平面$BCD$，$BC\subset$平面$BCD$，所以$AE\perp$平面$BCD$。因为$CD\subset$平面$BCD$，所以$AE\perp CD$。