《2025年世纪金榜新视野暑假作业高一数学》

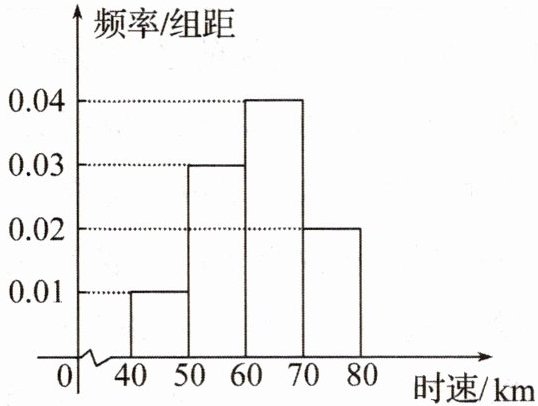
1.100辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则时速在$[60,70)$的汽车大约有 (B)

A.30辆
B.40辆
C.60辆
D.80辆

答案： 【解析】：
题目要求我们根据频率分布直方图来估计时速在$[60,70)$区间的汽车数量。
首先，我们需要确定这个区间的频率。
从直方图中，我们可以看到时速在$[60,70)$区间的频率/组距为0.04，
由于组距是10（每个区间都是10km/h），
所以该区间的频率是$0.04 × 10 = 0.4$，
然后，我们用这个频率来估计时速在$[60,70)$区间的汽车数量。
总共有100辆汽车，所以时速在$[60,70)$区间的汽车数量大约是$100 × 0.4 = 40$辆。
【答案】：B

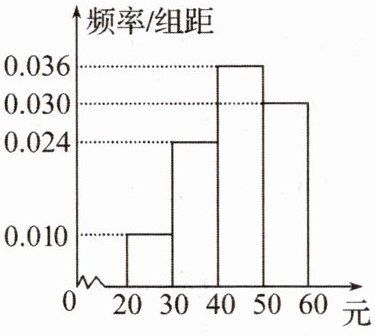
2.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在$[50,60]$元的同学有30人,则n的值为 (B)

A.90
B.100
C.900
D.1 000

答案： 【解析】：
本题考查频率分布直方图的应用，涉及频率、频数与样本容量的关系，属于基础题。
根据频率分布直方图，先求出支出在$[50,60]$元的频率，再结合已知该组的频数，利用频率与频数和样本容量的关系求出$n$的值。
计算支出在$[50,60]$元的频率：
在频率分布直方图中，每个小长方形的面积等于该组的频率。
已知频率分布直方图中组距为$10$，支出在$[50,60]$元对应的小长方形的高为$0.03$，
根据频率$=$小长方形的高$×$组距，可得支出在$[50,60]$元的频率为：$0.03×10 = 0.3$。
根据频率、频数与样本容量的关系求$n$的值：
频率、频数与样本容量的关系为：频率$=\frac{频数}{样本容量}$，已知支出在$[50,60]$元的同学有$30$人，即频数为$30$，设样本容量为$n$，
由上述关系可得$0.3=\frac{30}{n}$，解得$n = 100$。
【答案】：B。

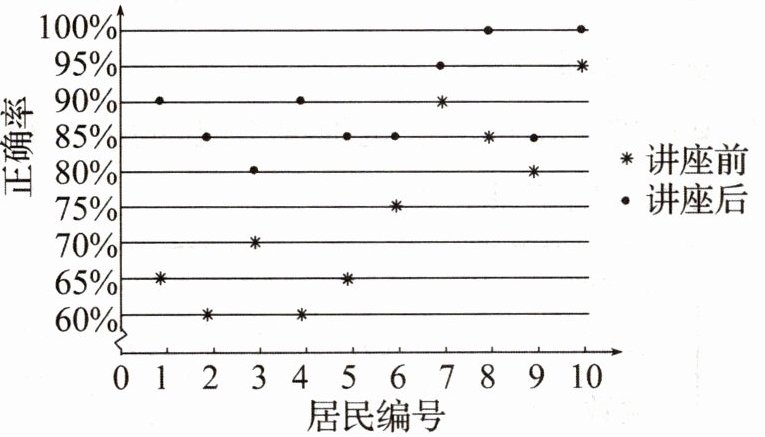
3.某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如图:

则 (B)
A.讲座前问卷答题的正确率的中位数小于70%
B.讲座后问卷答题的正确率的平均数大于85%
C.讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D.讲座后问卷答题的正确率的极差大于讲座前正确率的极差

答案： 【解析】：
本题考查的是对统计图的理解以及中位数、平均数、标准差和极差的计算。
A选项：计算讲座前问卷答题的正确率的中位数。
从图中可以看出，讲座前问卷答题的正确率从小到大排列为：$60\%,60\%,65\%,65\%,70\%,75\%,80\%,85\%,90\%,95\%$。
因为有10个数据，所以中位数是第5个和第6个数据的平均值，
即 $(70\% + 75\%) / 2 = 72.5\%$。
显然，$72.5\% ＞ 70\%$，
所以A选项错误。
B选项：计算讲座后问卷答题的正确率的平均数。
从图中可以看出，讲座后问卷答题的正确率分别为：$80\%,85\%,85\%,85\%,85\%,90\%,95\%,95\%,100\%,100\%$。
平均数为 $(80\% + 85\% × 4 + 90\% + 95\% × 2 + 100\% × 2) / 10 = 89\% ＞ 85\%$。
所以B选项正确。
C选项：比较讲座前后问卷答题的正确率的标准差。
标准差用于衡量数据的离散程度。
从图中可以看出，讲座前的数据更加分散，而讲座后的数据更加集中。
因此，讲座前问卷答题的正确率的标准差应该大于讲座后的标准差。
所以C选项错误。
D选项：比较讲座前后问卷答题的正确率的极差。
极差是数据中的最大值与最小值之差。
讲座前的极差为 $95\% - 60\% = 35\%$，
讲座后的极差为 $100\% - 80\% = 20\%$。
显然，讲座后的极差小于讲座前的极差。
所以D选项错误。
【答案】：B

4.某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则9时至14时的销售总额为 (D)
A.10万元
B.12万元
C.15万元
D.30万元

答案： 解：由频率分布直方图可知，9时至10时对应的频率/组距为0.10，组距为1，故该时间段的频率为0.10×1=0.10。
已知9时至10时销售额为3万元，设销售总额为$ x $万元，可得$ 0.10x = 3 $，解得$ x = 30 $。
D

5.某工厂对一批元件进行抽样检测.经检测,抽出的元件的长度(单位:mm)全部介于93至105之间.将抽出的元件的长度以2为组距分成6组:$[93,95),[95,97),[97,99),[99,101),[101,103),[103,105]$,得到如图所示的频率分布直方图.若长度在$[97,103)$内的元件为合格品,根据频率分布直方图,估计这批元件的合格率是 (A)
A.80%
B.90%
C.20%
D.85.5%

答案： 【解析】：
本题考查的知识点是频率分布直方图，解题的关键在于根据频率分布直方图计算合格品对应的频率。
已知长度在$[97,103)$内的元件为合格品，该区间包含$[97,99)$、$[99,101)$、$[101,103)$这三组。
在频率分布直方图中，频率$=$组距$×$频率/组距。
对于$[97,99)$这一组，组距为$2$，频率/组距为$0.1800$，则其频率为$2×0.1800 = 0.36$。
对于$[99,101)$这一组，组距为$2$，频率/组距为$0.1000$，则其频率为$2×0.1000 = 0.2$。
对于$[101,103)$这一组，组距为$2$，频率/组距为$0.0450$，则其频率为$2×0.0450 = 0.09$。
合格品的频率就是这三组频率之和，即$0.36 + 0.2 + 0.09 = 0.8$，将$0.8$转化为百分数为$80\%$，所以这批元件的合格率是$80\%$。
【答案】：
A