2025年世纪金榜新视野暑假作业高一数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年世纪金榜新视野暑假作业高一数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
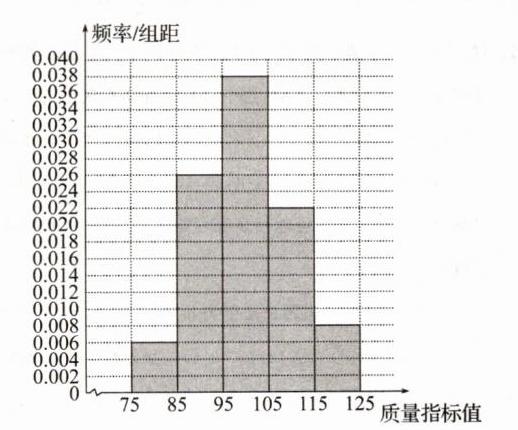
13.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得到如下频数分布表:
|质量指标值分组|$[75,85)$|$[85,95)$|$[95,105)$|$[105,115)$|$[115,125]$|
|频数|6|26|38|22|8|
(1)作出这些数据的频率分布直方图.
(2)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
|质量指标值分组|$[75,85)$|$[85,95)$|$[95,105)$|$[105,115)$|$[115,125]$|
|频数|6|26|38|22|8|
(1)作出这些数据的频率分布直方图.

(2)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
答案:
【解析】:
(1)
(2)我们需要计算质量指标值不低于95的产品所占的比例,
质量指标值不低于95的产品数量:$38+22+8=68$(件),
所占比例:$68/100=0.68$,或$68\%$,
由于$68\%<80\%$,
因此,根据以上抽样调查数据,不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的$80\%$”的规定。
【答案】:
(1)图略;
(2)根据以上抽样调查数据,不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的$80\%$”的规定。
【解析】:
(1)

(2)我们需要计算质量指标值不低于95的产品所占的比例,
质量指标值不低于95的产品数量:$38+22+8=68$(件),
所占比例:$68/100=0.68$,或$68\%$,
由于$68\%<80\%$,
因此,根据以上抽样调查数据,不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的$80\%$”的规定。
【答案】:
(1)图略;
(2)根据以上抽样调查数据,不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的$80\%$”的规定。
14.某经销商从外地一水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图.
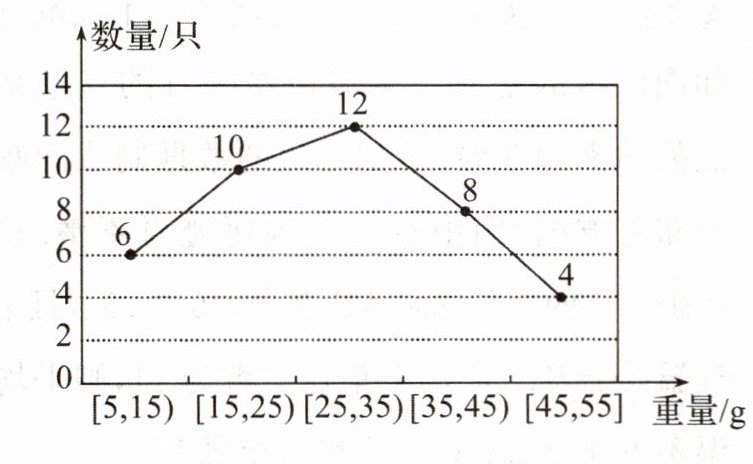
(1)估计这批小龙虾重量的第10百分位数与第90百分位数.
(2)该经销商将这批小龙虾分成三个等级,如表:
|等级|三等品|二等品|一等品|
|重量(g)|$[5,25)$|$[25,45)$|$[45,55]$|
试估计这批小龙虾划为几等品比较合理?

(1)估计这批小龙虾重量的第10百分位数与第90百分位数.
(2)该经销商将这批小龙虾分成三个等级,如表:
|等级|三等品|二等品|一等品|
|重量(g)|$[5,25)$|$[25,45)$|$[45,55]$|
试估计这批小龙虾划为几等品比较合理?
答案:
【解析】:
本题主要考查百分位数的计算以及用样本估计总体的思想。
(1)计算第$10$百分位数与第$90$百分位数:
首先,计算各区间的频率。
总数量$n = 40$只。
$[5,15)$区间的频率为$\frac{6}{40}=0.15$;
$[15,25)$区间的频率为$\frac{10}{40}=0.25$;
$[25,35)$区间的频率为$\frac{12}{40}=0.3$;
$[35,45)$区间的频率为$\frac{8}{40}=0.2$;
$[45,55]$区间的频率为$\frac{4}{40}=0.1$。
计算第$10$百分位数:
因为$40×10\% = 4$,说明第$10$百分位数位于$[5,15)$区间内。
设第$10$百分位数为$x$,由于$[5,15)$区间的频率为$0.15$,且该区间宽度为$10$,则$\frac{x - 5}{10}=\frac{4}{6}$(按比例计算),解得$x=\frac{20}{3}+5=\frac{35}{3}\approx11.67$。
计算第$90$百分位数:
因为$40×90\% = 36$,说明第$90$百分位数位于$[45,55]$区间内。
$[5,45)$区间的频率之和为$0.15 + 0.25+0.3 + 0.2=0.9$,$[45,55]$区间内$36-40×0.9=0$,说明第$90$百分位就是$45$。
(2)判断这批小龙虾的等级:
计算各等级的频率:
三等品$[5,25)$的频率为$0.15 + 0.25=0.4$;
二等品$[25,45)$的频率为$0.3+0.2 = 0.5$;
一等品$[45,55]$的频率为$0.1$。
根据频率大小判断,二等品的频率最大,所以估计这批小龙虾划为二等品比较合理。
【答案】:
(1)这批小龙虾重量的第$10$百分位数约为$11.67$,第$90$百分位数是$45$;
(2)估计这批小龙虾划为二等品比较合理。
本题主要考查百分位数的计算以及用样本估计总体的思想。
(1)计算第$10$百分位数与第$90$百分位数:
首先,计算各区间的频率。
总数量$n = 40$只。
$[5,15)$区间的频率为$\frac{6}{40}=0.15$;
$[15,25)$区间的频率为$\frac{10}{40}=0.25$;
$[25,35)$区间的频率为$\frac{12}{40}=0.3$;
$[35,45)$区间的频率为$\frac{8}{40}=0.2$;
$[45,55]$区间的频率为$\frac{4}{40}=0.1$。
计算第$10$百分位数:
因为$40×10\% = 4$,说明第$10$百分位数位于$[5,15)$区间内。
设第$10$百分位数为$x$,由于$[5,15)$区间的频率为$0.15$,且该区间宽度为$10$,则$\frac{x - 5}{10}=\frac{4}{6}$(按比例计算),解得$x=\frac{20}{3}+5=\frac{35}{3}\approx11.67$。
计算第$90$百分位数:
因为$40×90\% = 36$,说明第$90$百分位数位于$[45,55]$区间内。
$[5,45)$区间的频率之和为$0.15 + 0.25+0.3 + 0.2=0.9$,$[45,55]$区间内$36-40×0.9=0$,说明第$90$百分位就是$45$。
(2)判断这批小龙虾的等级:
计算各等级的频率:
三等品$[5,25)$的频率为$0.15 + 0.25=0.4$;
二等品$[25,45)$的频率为$0.3+0.2 = 0.5$;
一等品$[45,55]$的频率为$0.1$。
根据频率大小判断,二等品的频率最大,所以估计这批小龙虾划为二等品比较合理。
【答案】:
(1)这批小龙虾重量的第$10$百分位数约为$11.67$,第$90$百分位数是$45$;
(2)估计这批小龙虾划为二等品比较合理。
15.某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.
(1)估计高一参赛学生的成绩的众数、中位数.
(2)估计高一参赛学生的平均成绩.
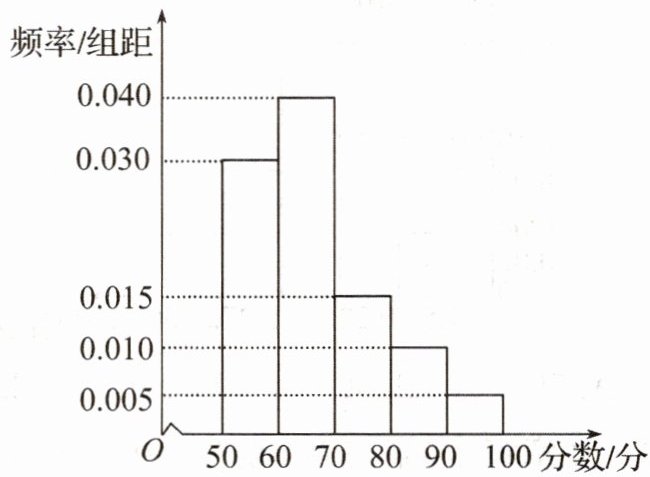
(1)估计高一参赛学生的成绩的众数、中位数.
(2)估计高一参赛学生的平均成绩.

答案:
【解析】:
(1)求众数:
众数是一组数据中出现次数最多的数值。
在频率分布直方图中,频率最高的小组的中点值即为众数。
从图中可以看出,第二小组的频率最高,为0.40,其对应的分数范围是60-70分。
因此,众数为 $(60+70)÷2=65$(分)。
求中位数:
中位数是将一组数据从小到大排列后,位于中间位置的数值。
在频率分布直方图中,中位数是将频率分布直方图划分为面积相等的两部分的那个数值。
已知各小组的频率分别为0.30、0.40、0.15、0.10、0.05。
前两组的频率和为0.30+0.40=0.70,已经超过了0.50,所以中位数在第二小组内。
设中位数为$x$,则有:
$0.30+(x-60)×0.04=0.50$。
解得$x=65$。
所以,中位数为65分(由于我们是在连续分布的假设下进行计算,这个值是一个估计值)。
(2)求平均成绩:
平均成绩是所有数据之和除以数据的数量。
在频率分布直方图中,可以使用各小组的中点值乘以该小组的频率,然后将这些乘积相加,得到平均成绩的估计值。
$\text{平均成绩} = 55 × 0.30 + 65 × 0.40 + 75 × 0.15 + 85 × 0.10 + 95 × 0.05=67$(分)。
【答案】:
(1)众数为65分,中位数为65分;
(2)高一参赛学生的平均成绩为67分。
(1)求众数:
众数是一组数据中出现次数最多的数值。
在频率分布直方图中,频率最高的小组的中点值即为众数。
从图中可以看出,第二小组的频率最高,为0.40,其对应的分数范围是60-70分。
因此,众数为 $(60+70)÷2=65$(分)。
求中位数:
中位数是将一组数据从小到大排列后,位于中间位置的数值。
在频率分布直方图中,中位数是将频率分布直方图划分为面积相等的两部分的那个数值。
已知各小组的频率分别为0.30、0.40、0.15、0.10、0.05。
前两组的频率和为0.30+0.40=0.70,已经超过了0.50,所以中位数在第二小组内。
设中位数为$x$,则有:
$0.30+(x-60)×0.04=0.50$。
解得$x=65$。
所以,中位数为65分(由于我们是在连续分布的假设下进行计算,这个值是一个估计值)。
(2)求平均成绩:
平均成绩是所有数据之和除以数据的数量。
在频率分布直方图中,可以使用各小组的中点值乘以该小组的频率,然后将这些乘积相加,得到平均成绩的估计值。
$\text{平均成绩} = 55 × 0.30 + 65 × 0.40 + 75 × 0.15 + 85 × 0.10 + 95 × 0.05=67$(分)。
【答案】:
(1)众数为65分,中位数为65分;
(2)高一参赛学生的平均成绩为67分。
查看更多完整答案,请扫码查看


