2025年世纪金榜新视野暑假作业高一数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年世纪金榜新视野暑假作业高一数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
10. 如图,$\overrightarrow{AO}$是某人行走的路线,那么$\overrightarrow{AO}的几何意义是某人从A$点沿西偏南
$60^\circ$
方向行走了$2$
$km$.
答案:
【解析】:
本题主要考查平面向量的概念,特别是向量的方向和模长。
根据题目中的图,可以看出向量$\overrightarrow{AO}$是从点$A$指向原点$O$。
由于$AO$与正东方向($x$轴正方向)的夹角为$60^\circ$,
因此,从$A$点出发沿这个方向行走,实际上是西偏南$60^\circ$方向(因为是从东方向往回走,所以是西偏)。
向量的模长即为行走的距离,图中明确标注了$A$到$O$的距离为$2km$。
【答案】:
$60^\circ$;$2$。
本题主要考查平面向量的概念,特别是向量的方向和模长。
根据题目中的图,可以看出向量$\overrightarrow{AO}$是从点$A$指向原点$O$。
由于$AO$与正东方向($x$轴正方向)的夹角为$60^\circ$,
因此,从$A$点出发沿这个方向行走,实际上是西偏南$60^\circ$方向(因为是从东方向往回走,所以是西偏)。
向量的模长即为行走的距离,图中明确标注了$A$到$O$的距离为$2km$。
【答案】:
$60^\circ$;$2$。
11. 已知$A$,$B$,$C$是不共线的三点,向量$\boldsymbol{m}与向量\overrightarrow{AB}$是平行向量,与$\overrightarrow{BC}$是共线向量,则$\boldsymbol{m}= $
$\boldsymbol{0}$
.
答案:
【解析】:
本题主要考查平面向量的基本概念和性质。
首先,根据题目条件,向量$\boldsymbol{m}$与向量$\overrightarrow{AB}$是平行向量。在平面向量中,平行向量意味着两个向量在同一直线或平行直线上,但方向可以相同或相反。
其次,题目还给出向量$\boldsymbol{m}$与向量$\overrightarrow{BC}$是共线向量。共线向量是方向相同或相反的非零向量,或者其中一个向量是零向量。
然而,题目中明确给出$A$, $B$, $C$是不共线的三点。这意味着三点不构成一条直线,因此,$\overrightarrow{AB}$和$\overrightarrow{BC}$不共线。
由于向量$\boldsymbol{m}$同时与$\overrightarrow{AB}$和$\overrightarrow{BC}$平行(或共线),但$\overrightarrow{AB}$和$\overrightarrow{BC}$不共线,这在平面向量中是一个矛盾的情况,除非$\boldsymbol{m}$是零向量。因为零向量与任何向量都平行且共线。
所以,根据这些分析,我们可以得出结论:$\boldsymbol{m} = \boldsymbol{0}$(零向量)。
【答案】:
$\boldsymbol{0}$
本题主要考查平面向量的基本概念和性质。
首先,根据题目条件,向量$\boldsymbol{m}$与向量$\overrightarrow{AB}$是平行向量。在平面向量中,平行向量意味着两个向量在同一直线或平行直线上,但方向可以相同或相反。
其次,题目还给出向量$\boldsymbol{m}$与向量$\overrightarrow{BC}$是共线向量。共线向量是方向相同或相反的非零向量,或者其中一个向量是零向量。
然而,题目中明确给出$A$, $B$, $C$是不共线的三点。这意味着三点不构成一条直线,因此,$\overrightarrow{AB}$和$\overrightarrow{BC}$不共线。
由于向量$\boldsymbol{m}$同时与$\overrightarrow{AB}$和$\overrightarrow{BC}$平行(或共线),但$\overrightarrow{AB}$和$\overrightarrow{BC}$不共线,这在平面向量中是一个矛盾的情况,除非$\boldsymbol{m}$是零向量。因为零向量与任何向量都平行且共线。
所以,根据这些分析,我们可以得出结论:$\boldsymbol{m} = \boldsymbol{0}$(零向量)。
【答案】:
$\boldsymbol{0}$
12. 如果在一个边长为5的正$\triangle ABC$中,一个向量所对应的有向线段为$\overrightarrow{AD}$(其中$D在边BC$上运动),则向量$\overrightarrow{AD}$长度的最小值为
$\frac{5\sqrt{3}}{2}$
.
答案:
【解析】:
本题主要考察平面向量的模长计算以及其在几何中的应用。
首先,由于$\triangle ABC$是等边三角形,所以$AB = AC = BC = 5$。
当$AD$垂直于$BC$时,$AD$的长度最小。这是因为,在给定起点$A$和终点$D$在直线$BC$上的情况下,垂直于$BC$的线段$AD$是最短的。
在等边三角形中,高$AD$可以通过以下公式计算:
$AD = AB × \sin 60^\circ = 5 × \frac{\sqrt{3}}{2} = \frac{5\sqrt{3}}{2}$,
其中,$\sin 60^\circ = \frac{\sqrt{3}}{2}$是等边三角形中一个内角的正弦值。
【答案】:
$\frac{5\sqrt{3}}{2}$。
本题主要考察平面向量的模长计算以及其在几何中的应用。
首先,由于$\triangle ABC$是等边三角形,所以$AB = AC = BC = 5$。
当$AD$垂直于$BC$时,$AD$的长度最小。这是因为,在给定起点$A$和终点$D$在直线$BC$上的情况下,垂直于$BC$的线段$AD$是最短的。
在等边三角形中,高$AD$可以通过以下公式计算:
$AD = AB × \sin 60^\circ = 5 × \frac{\sqrt{3}}{2} = \frac{5\sqrt{3}}{2}$,
其中,$\sin 60^\circ = \frac{\sqrt{3}}{2}$是等边三角形中一个内角的正弦值。
【答案】:
$\frac{5\sqrt{3}}{2}$。
13. 如图是中国象棋的半个棋盘,“马走日”是象棋中马的走法.此图中,马可以从$A处跳到A_1$处,用向量$\overrightarrow{AA_1}$表示马走了“一步”,也可以跳到$A_2$处,用向量$\overrightarrow{AA_2}$表示. 请在图中画出马在$B$,$C$处走了“一步”的所有情况.
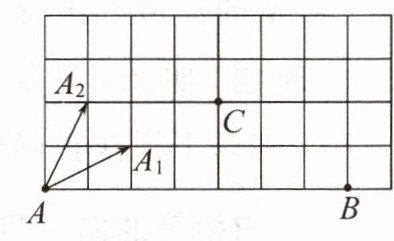

答案:


14. 设在平面内给定一个四边形$ABCD$,$E$,$F$,$G$,$H分别为AB$,$BC$,$CD$,$DA$的中点.
求证:$\overrightarrow{EF}= \overrightarrow{HG}$.
求证:$\overrightarrow{EF}= \overrightarrow{HG}$.
答案:
证明:连接AC。
在△ABC中,E,F分别为AB,BC的中点,
根据三角形中位线定理,EF//AC且EF = $\frac{1}{2}$AC,
所以$\overrightarrow{EF} = \frac{1}{2}\overrightarrow{AC}$。
在△ADC中,H,G分别为DA,CD的中点,
同理可得HG//AC且HG = $\frac{1}{2}$AC,
所以$\overrightarrow{HG} = \frac{1}{2}\overrightarrow{AC}$。
因此,$\overrightarrow{EF} = \overrightarrow{HG}$。
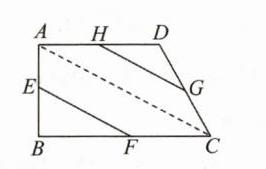
证明:连接AC。
在△ABC中,E,F分别为AB,BC的中点,
根据三角形中位线定理,EF//AC且EF = $\frac{1}{2}$AC,
所以$\overrightarrow{EF} = \frac{1}{2}\overrightarrow{AC}$。
在△ADC中,H,G分别为DA,CD的中点,
同理可得HG//AC且HG = $\frac{1}{2}$AC,
所以$\overrightarrow{HG} = \frac{1}{2}\overrightarrow{AC}$。
因此,$\overrightarrow{EF} = \overrightarrow{HG}$。

15. 一辆汽车从$A点出发向西行驶了100\ km到达B$点,然后又改变方向向西偏北$50^{\circ}行驶了200\ km到达C$点,最后又改变方向,向东行驶了$100\ km到达D$点.
(1)作出向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{CD}$.
(2)求这辆汽车的位移大小.
(1)作出向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{CD}$.
(2)求这辆汽车的位移大小.
答案:
(1) (由于无法直接作图,此处略去图形绘制步骤,实际作答时需按题目要求画出向量$\overrightarrow{AB}$(方向向西,长度表示100km)、$\overrightarrow{BC}$(方向西偏北$50^{\circ}$,长度表示200km)、$\overrightarrow{CD}$(方向向东,长度表示100km))
(2) 解:由题意可知,汽车从A点向西行驶100km到B点,再向东行驶100km到D点,所以$\overrightarrow{AB}$与$\overrightarrow{CD}$大小相等,方向相反,即$\overrightarrow{AB}=-\overrightarrow{CD}$,所以$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{BC}$。因为$\overrightarrow{BC}$的长度为200km,所以这辆汽车的位移大小为200km。
答:这辆汽车的位移大小为200km。
(1) (由于无法直接作图,此处略去图形绘制步骤,实际作答时需按题目要求画出向量$\overrightarrow{AB}$(方向向西,长度表示100km)、$\overrightarrow{BC}$(方向西偏北$50^{\circ}$,长度表示200km)、$\overrightarrow{CD}$(方向向东,长度表示100km))
(2) 解:由题意可知,汽车从A点向西行驶100km到B点,再向东行驶100km到D点,所以$\overrightarrow{AB}$与$\overrightarrow{CD}$大小相等,方向相反,即$\overrightarrow{AB}=-\overrightarrow{CD}$,所以$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{BC}$。因为$\overrightarrow{BC}$的长度为200km,所以这辆汽车的位移大小为200km。
答:这辆汽车的位移大小为200km。
查看更多完整答案,请扫码查看


