《2025年世纪金榜新视野暑假作业高一数学》

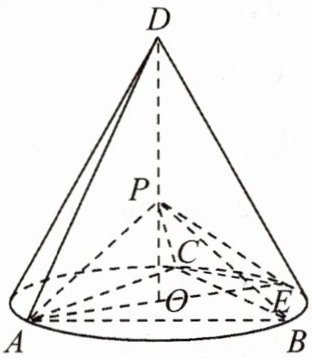
16.如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE= AD.△ABC是底面的内接正三角形,P为DO上一点,$PO= \frac {\sqrt {6}}{6}DO$.
(1)证明:PA⊥平面PBC;
(2)求二面角B-PC-E的余弦值.

答案： 1. （1）证明：
设$DO = a$，由$PO=\frac{\sqrt{6}}{6}DO$，可得$PO = \frac{\sqrt{6}}{6}a$，$AO=\frac{1}{2}AE$，因为$AE = AD$，在$Rt\triangle AOD$中，$AO=\frac{\sqrt{2}}{2}AD$（根据勾股定理$AO^{2}+DO^{2}=AD^{2}$，且$AE = AD$，$AO=\frac{1}{2}AE$），设$AO = r$，则$AD = 2r$，$DO=\sqrt{AD^{2}-AO^{2}}=\sqrt{3}r$，所以$PO=\frac{\sqrt{6}}{6}×\sqrt{3}r=\frac{\sqrt{2}}{2}r$。
因为$\triangle ABC$是正三角形，$AE$是直径，所以$\angle ACB = 90^{\circ}$，$\angle CAB = 60^{\circ}$，$CA = CB$。
计算$PA$，$PB$，$PC$的长度：
在$Rt\triangle PAO$中，$PA=\sqrt{AO^{2}+PO^{2}}=\sqrt{r^{2}+\frac{1}{2}r^{2}}=\frac{\sqrt{6}}{2}r$。
连接$OB$，$OC$，因为$OB = OC = r$，$PO\perp$底面$ABC$，根据勾股定理$PB=\sqrt{PO^{2}+OB^{2}}=\sqrt{\frac{1}{2}r^{2}+r^{2}}=\frac{\sqrt{6}}{2}r$，$PC=\sqrt{PO^{2}+OC^{2}}=\frac{\sqrt{6}}{2}r$。
计算向量的数量积（也可用勾股定理逆定理）：
$PA^{2}+PB^{2}=(\frac{\sqrt{6}}{2}r)^{2}+(\frac{\sqrt{6}}{2}r)^{2}=3r^{2}$，$AB = 2r\sin60^{\circ}=\sqrt{3}r$，$PA^{2}+PC^{2}=3r^{2}$，$AC=\sqrt{3}r$。
又$PA^{2}+PB^{2}=AB^{2}$，所以$PA\perp PB$；$PA^{2}+PC^{2}=AC^{2}$，所以$PA\perp PC$。
因为$PB\cap PC = P$，$PB,PC\subset$平面$PBC$，所以$PA\perp$平面$PBC$。
2. （2）
以$O$为坐标原点，$\overrightarrow{OE}$，$\overrightarrow{OB}$，$\overrightarrow{OP}$的方向分别为$x$，$y$，$z$轴正方向建立空间直角坐标系。
设$r = 1$，则$O(0,0,0)$，$P(0,0,\frac{\sqrt{2}}{2})$，$B(0,1,0)$，$C(-\frac{\sqrt{3}}{2},\frac{1}{2},0)$，$E(1,0,0)$。
求平面$BPC$和平面$EPC$的法向量：
$\overrightarrow{PB}=(0,1,-\frac{\sqrt{2}}{2})$，$\overrightarrow{PC}=(-\frac{\sqrt{3}}{2},\frac{1}{2},-\frac{\sqrt{2}}{2})$。
设平面$BPC$的法向量$\overrightarrow{n_{1}}=(x_{1},y_{1},z_{1})$，则$\begin{cases}\overrightarrow{n_{1}}\cdot\overrightarrow{PB}=y_{1}-\frac{\sqrt{2}}{2}z_{1}=0\\\overrightarrow{n_{1}}\cdot\overrightarrow{PC}=-\frac{\sqrt{3}}{2}x_{1}+\frac{1}{2}y_{1}-\frac{\sqrt{2}}{2}z_{1}=0\end{cases}$，令$z_{1}=\sqrt{2}$，则$y_{1}=1$，$x_{1}=-\frac{\sqrt{3}}{3}$，所以$\overrightarrow{n_{1}}=(-\frac{\sqrt{3}}{3},1,\sqrt{2})$。
$\overrightarrow{PC}=(-\frac{\sqrt{3}}{2},\frac{1}{2},-\frac{\sqrt{2}}{2})$，$\overrightarrow{PE}=(1,0,-\frac{\sqrt{2}}{2})$。
设平面$EPC$的法向量$\overrightarrow{n_{2}}=(x_{2},y_{2},z_{2})$，则$\begin{cases}\overrightarrow{n_{2}}\cdot\overrightarrow{PC}=-\frac{\sqrt{3}}{2}x_{2}+\frac{1}{2}y_{2}-\frac{\sqrt{2}}{2}z_{2}=0\\\overrightarrow{n_{2}}\cdot\overrightarrow{PE}=x_{2}-\frac{\sqrt{2}}{2}z_{2}=0\end{cases}$，令$z_{2}=\sqrt{2}$，则$x_{2}=1$，$y_{2}=\sqrt{3}$，所以$\overrightarrow{n_{2}}=(1,\sqrt{3},\sqrt{2})$。
计算二面角的余弦值：
根据$\cos\langle\overrightarrow{n_{1}},\overrightarrow{n_{2}}\rangle=\frac{\overrightarrow{n_{1}}\cdot\overrightarrow{n_{2}}}{\vert\overrightarrow{n_{1}}\vert\vert\overrightarrow{n_{2}}\vert}$。
$\overrightarrow{n_{1}}\cdot\overrightarrow{n_{2}}=-\frac{\sqrt{3}}{3}×1 + 1×\sqrt{3}+\sqrt{2}×\sqrt{2}=\frac{2\sqrt{3}}{3}+2$，$\vert\overrightarrow{n_{1}}\vert=\sqrt{\frac{1}{3}+1 + 2}=\sqrt{\frac{1 + 3+6}{3}}=\frac{\sqrt{30}}{3}$，$\vert\overrightarrow{n_{2}}\vert=\sqrt{1 + 3+2}=\sqrt{6}$。
$\cos\langle\overrightarrow{n_{1}},\overrightarrow{n_{2}}\rangle=\frac{\overrightarrow{n_{1}}\cdot\overrightarrow{n_{2}}}{\vert\overrightarrow{n_{1}}\vert\vert\overrightarrow{n_{2}}\vert}=\frac{\frac{2\sqrt{3}}{3}+2}{\frac{\sqrt{30}}{3}×\sqrt{6}}=\frac{\sqrt{5}}{5}$。
观察二面角$B - PC - E$是锐角，所以二面角$B - PC - E$的余弦值为$\frac{\sqrt{5}}{5}$。
综上，（1）证明见上述过程；（2）二面角$B - PC - E$的余弦值为$\boldsymbol{\frac{\sqrt{5}}{5}}$。

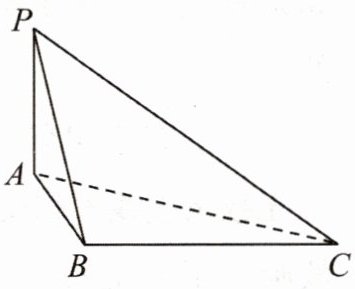
17.如图,在四面体P-ABC中,PA⊥平面ABC,PA= AB= 1,$BC= \sqrt {3},AC= 2$.
(1)证明:BC⊥平面PAB.
(2)在线段PC上是否存在点D,使得AC⊥BD,若存在,求PD的值,若不存在,请说明理由.

答案： 【解析】：
(1)本题可根据线面垂直的判定定理来证明$BC\perp$平面$PAB$，需要先在$\triangle ABC$中证明$BC\perp AB$，再结合已知条件$PA\perp$平面$ABC$得到$PA\perp BC$，最后根据线面垂直的判定定理得出结论。
在$\triangle ABC$中，已知$AB = 1$，$BC = \sqrt{3}$，$AC = 2$，根据勾股定理的逆定理，判断$AB^{2}+BC^{2}$与$AC^{2}$的关系：
$AB^{2}+BC^{2}=1^{2}+(\sqrt{3})^{2}=1 + 3 = 4$，而$AC^{2}=2^{2}=4$，所以$AB^{2}+BC^{2}=AC^{2}$，则$\triangle ABC$是直角三角形，且$\angle ABC = 90^{\circ}$，即$BC\perp AB$。
因为$PA\perp$平面$ABC$，$BC\subset$平面$ABC$，根据线面垂直的性质可知$PA\perp BC$。
又因为$PA\cap AB = A$，$PA\subset$平面$PAB$，$AB\subset$平面$PAB$，根据直线与平面垂直的判定定理：如果一条直线与平面内两条相交直线都垂直，那么这条直线与这个平面垂直，所以$BC\perp$平面$PAB$。
(2)本题可通过建立空间直角坐标系，利用向量垂直的性质来求解。先求出相关点的坐标，再设出点$D$的坐标，根据向量垂直的性质列出方程，求解出点$D$的位置，进而求出$PD$的值。
以$A$为原点，分别以$AB$，$AC$，$AP$所在直线为$x$，$y$，$z$轴建立空间直角坐标系。
已知$PA = AB = 1$，$BC = \sqrt{3}$，$AC = 2$，则$A(0,0,0)$，$B(1,0,0)$，$C(0,2,0)$，$P(0,0,1)$。
设$\overrightarrow{PD}=\lambda\overrightarrow{PC}(0\leqslant\lambda\leqslant1)$，先求出$\overrightarrow{PC}$的坐标：$\overrightarrow{PC}=(0 - 0,2 - 0,0 - 1)=(0,2,-1)$。
则$\overrightarrow{PD}=\lambda(0,2,-1)=(0,2\lambda,-\lambda)$，又因为$\overrightarrow{AP}=(0,0,1)$，所以$\overrightarrow{AD}=\overrightarrow{AP}+\overrightarrow{PD}=(0,0,1)+(0,2\lambda,-\lambda)=(0,2\lambda,1 - \lambda)$，那么点$D$的坐标为$(0,2\lambda,1 - \lambda)$。
所以$\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}=(0,2\lambda,1 - \lambda)-(1,0,0)=(-1,2\lambda,1 - \lambda)$，$\overrightarrow{AC}=(0,2,0)$。
因为$AC\perp BD$，所以$\overrightarrow{AC}\cdot\overrightarrow{BD}=0$，根据向量数量积的坐标运算公式：若$\overrightarrow{a}=(x_1,y_1,z_1)$，$\overrightarrow{b}=(x_2,y_2,z_2)$，则$\overrightarrow{a}\cdot\overrightarrow{b}=x_1x_2 + y_1y_2 + z_1z_2$，可得：
$\overrightarrow{AC}\cdot\overrightarrow{BD}=0×(-1)+2×2\lambda + 0×(1 - \lambda)=4\lambda = 0$，解得$\lambda = \frac{1}{4}$。
$\overrightarrow{PC}=(0,2,-1)$，则$\overrightarrow{PD}=\frac{1}{4}\overrightarrow{PC}$，所以$\vert\overrightarrow{PD}\vert=\frac{1}{4}\vert\overrightarrow{PC}\vert$。
根据空间两点间距离公式求$\vert\overrightarrow{PC}\vert$：$\vert\overrightarrow{PC}\vert=\sqrt{0^{2}+2^{2}+(-1)^{2}}=\sqrt{4 + 1}=\sqrt{5}$，则$\vert\overrightarrow{PD}\vert=\frac{1}{4}×\sqrt{5}=\frac{\sqrt{5}}{4}$。
【答案】：
(1)证明：在$\triangle ABC$中，因为$AB = 1$，$BC = \sqrt{3}$，$AC = 2$，所以$AB^{2}+BC^{2}=AC^{2}$，则$\angle ABC = 90^{\circ}$，即$BC\perp AB$。
又因为$PA\perp$平面$ABC$，$BC\subset$平面$ABC$，所以$PA\perp BC$。
且$PA\cap AB = A$，$PA\subset$平面$PAB$，$AB\subset$平面$PAB$，所以$BC\perp$平面$PAB$。
(2)存在点$D$，使得$AC\perp BD$，$PD=\frac{\sqrt{5}}{4}$。