《2025年启东中学作业本八年级数学上册苏科版徐州专版》

两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS”).

答案： 对边 AAS

1. 如图,AC是$∠BAE$的平分线,D是线段AC上一点,$∠C= ∠E,AB= AD.$
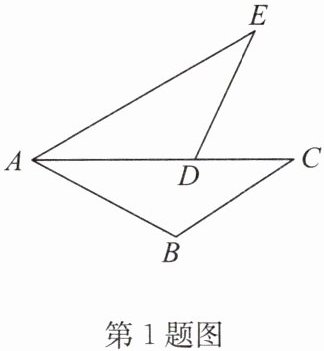
求证:$BC= DE.$

答案： 证明:
∵AC 是∠BAE 的平分线,
∴∠BAC=∠DAE.
在△BAC 和△DAE 中,$\left\{\begin{array}{l} ∠BAC=∠DAE,\\ ∠C=∠E,\\ AB=AD,\end{array}\right. $
∴△BAC≌△DAE(AAS),
∴BC=DE.

2. 如图,$∠BAC= 90^{\circ }$,AD是$∠BAC$内部一条射线,若$AB= AC,BE⊥AD$于点E,$CF⊥AD$于点F. 求证:$\triangle ABE\cong \triangle CAF.$

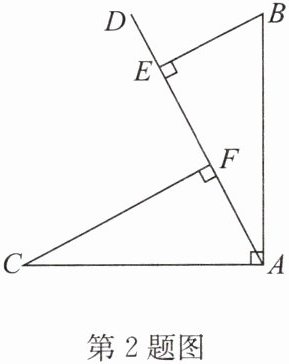
答案： 证明:
∵∠BAC=90°,
∴∠CAF+∠BAE=90°.
∵BE⊥AD,CF⊥AD,
∴∠CFA=∠BEA=90°,
∴∠C+∠CAF=90°,
∴∠C=∠BAE.
在△ABE 和△CAF 中,$\left\{\begin{array}{l} ∠BEA=∠AFC,\\ ∠BAE=∠C,\\ AB=CA,\end{array}\right. $
∴△ABE≌△CAF(AAS).

3. 如图,在四边形ABCD中,$AD// BC,AE⊥AD$交BD于点E,$CF⊥BC$交BD于点F,且$AE= CF.$
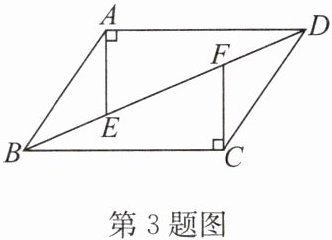
求证:(1)$\triangle ADE\cong \triangle CBF;$
(2)$AB= CD.$

答案： 证明:
(1)
∵AD//BC,
∴∠ADE=∠CBF.
∵AE⊥AD,CF⊥BC,
∴∠EAD=∠FCB=90°.
在△ADE 和△CBF 中,$\left\{\begin{array}{l} ∠ADE=∠CBF,\\ ∠EAD=∠FCB,\\ AE=CF,\end{array}\right. $
∴△ADE≌△CBF(AAS).
(2)
∵△ADE≌△CBF,
∴AD=BC.
在△ABD 和△CDB 中,$\left\{\begin{array}{l} AD=CB,\\ ∠ADB=∠CBD,\\ BD=DB,\end{array}\right. $
∴△ABD≌△CDB(SAS),
∴AB=CD.