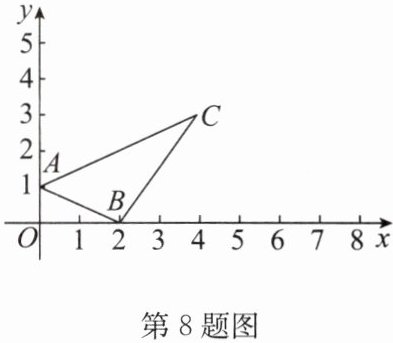
8. 将$\triangle ABC$放在如图所示的平面直角坐标系中。
(1)写出$\triangle ABC$三个顶点的坐标;
(2)求$\triangle ABC$的面积;
(3)设点P在x轴上,且$\triangle ABP与\triangle ABC$的面积相等,求点P的坐标。
(1)写出$\triangle ABC$三个顶点的坐标;
(2)求$\triangle ABC$的面积;
(3)设点P在x轴上,且$\triangle ABP与\triangle ABC$的面积相等,求点P的坐标。

答案:
解:
(1)A(0,1),B(2,0),C(4,3).
(2)如答图,过点C作CD⊥x轴,CE⊥y,垂足分别为D,E
S△ABC=S四边形DCEO - S△AEC - S△ABO - S△BCD
=3×4 - $\frac{1}{2}$×2×4 - $\frac{1}{2}$×1×2 - $\frac{1}{2}$×2×3
=12 - 4 - 1 - 3 = 4.
(3)设点P的坐标为(x,0),则BP = |x - 2|.
∵△ABP与△ABC的面积相等,
∴$\frac{1}{2}$×1×|x - 2| = 4,解得x = 10或x = - 6.
∴点P的坐标为(10,0)或(- 6,0).
解:
(1)A(0,1),B(2,0),C(4,3).
(2)如答图,过点C作CD⊥x轴,CE⊥y,垂足分别为D,E

S△ABC=S四边形DCEO - S△AEC - S△ABO - S△BCD
=3×4 - $\frac{1}{2}$×2×4 - $\frac{1}{2}$×1×2 - $\frac{1}{2}$×2×3
=12 - 4 - 1 - 3 = 4.
(3)设点P的坐标为(x,0),则BP = |x - 2|.
∵△ABP与△ABC的面积相等,
∴$\frac{1}{2}$×1×|x - 2| = 4,解得x = 10或x = - 6.
∴点P的坐标为(10,0)或(- 6,0).
根据实际问题的需要,建立合适的平面直角坐标系,更便于研究和解决问题。一般,利用实际问题中图形中的直角(包括隐含的直角),以直角顶点为
原点
,两直角边所在直线分别为x
轴、y
轴,建立平面直角坐标系。
答案:
原点 x y
1. 小米家位于公园的正东100米处,从小米家出发向北走250米就到小华家,若选取小华家为原点,分别以正东、正北方向为x轴,y轴正方向建立平面直角坐标系,则公园的坐标是(
A.$(-250,-100)$
B.$(100,250)$
C.$(-100,-250)$
D.$(250,100)$
C
)A.$(-250,-100)$
B.$(100,250)$
C.$(-100,-250)$
D.$(250,100)$
答案:
C
查看更多完整答案,请扫码查看


