《2025年启东中学作业本八年级数学上册苏科版徐州专版》

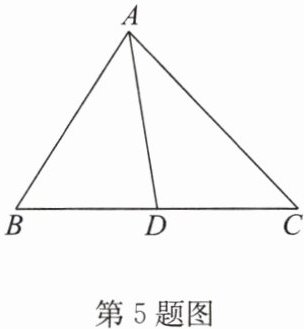
5. (苏州期末)如图,已知△ABC的周长为21 cm,AB= 6 cm,BC边上中线AD= 5 cm,△ABD周长为15 cm,求AC的长.

答案： 解：
∵AB=6 cm，AD=5 cm，△ABD 周长为 15 cm，
∴BD=15-6-5=4(cm).
∵AD 是 BC 边上的中线，
∴BC=8 cm.
∵△ABC 的周长为 21 cm，
∴AC=21-6-8=7(cm).

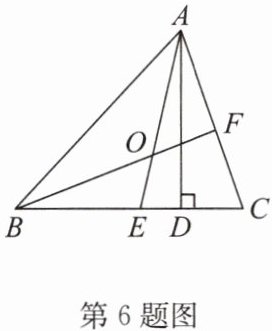
6. 如图,在△ABC中,AD是高线,AE,BF是角平分线,它们相交于点O,∠BAC= 60°,∠C= 70°,求∠EAD,∠BOA的度数.

答案： 解：
∵AD⊥BC，
∴∠ADC=90°.
∵∠C=70°，
∴∠DAC=180°-90°-70°=20°.
∵AE 平分∠BAC，
∴∠CAE=$\frac{1}{2}$×60°=30°，
∴∠EAD=∠EAC-∠DAC=30°-20°=10°.
∵∠BAC=60°，∠C=70°，
∴∠BAO=30°，∠ABC=50°.
∵BF 是∠ABC 的平分线，
∴∠ABO=25°
∴∠BOA=180°-∠BAO-∠ABO=180°-25°-30°=125°.