有两个角
相等
的三角形是等腰三角形(简称“等角对等边”).
答案:
相等
1. 在$\triangle ABC$中,已知$∠B= ∠C$,则 (
A.$AB= BC$
B.$AB= AC$
C.$BC= AC$
D.$∠A= 60^{\circ }$
B
)A.$AB= BC$
B.$AB= AC$
C.$BC= AC$
D.$∠A= 60^{\circ }$
答案:
B
2. 若长度分别为 3,1,x 的三条线段能组成一个等腰三角形,则 x 的值可以是 (
A.1
B.3
C.1 或 3
D.不存在
B
)A.1
B.3
C.1 或 3
D.不存在
答案:
B
3. 如图,$∠A= 36^{\circ },∠DBC= 36^{\circ },∠C= 72^{\circ }$,则图中等腰三角形有
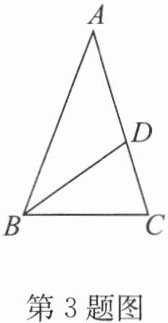
3
个.
答案:
3
4. 如图,CD 平分$∠ACE$,且$AB// CD$,求证:$\triangle ABC$为等腰三角形.
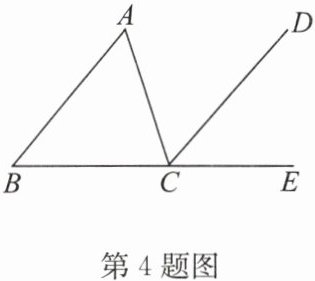

答案:
证明:
∵AB//CD,
∴∠A=∠ACD,∠B=∠DCE.
∵CD平分∠ACE,
∴∠ACD=∠DCE,
∴∠B=∠A,
∴AC=BC,
∴△ABC为等腰三角形.
∵AB//CD,
∴∠A=∠ACD,∠B=∠DCE.
∵CD平分∠ACE,
∴∠ACD=∠DCE,
∴∠B=∠A,
∴AC=BC,
∴△ABC为等腰三角形.
5. 如图,在$\triangle ABC$中,$AB= AC$,BD 与 CE 相交于点 O,且$EB= DC$. 求证:$\triangle BOC$是等腰三角形.
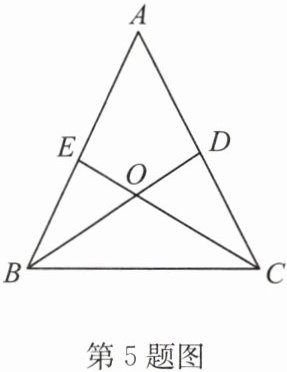

答案:
证明:
∵AB=AC,
∴∠ABC=∠ACB.在△BEC和△CDB中,EB=DC,∠ABC=∠ACB,BC=CB,
∴△BEC≌△CDB(SAS),
∴∠ECB=∠DBC,
∴OB=OC,
∴△BOC是等腰三角形.
∵AB=AC,
∴∠ABC=∠ACB.在△BEC和△CDB中,EB=DC,∠ABC=∠ACB,BC=CB,
∴△BEC≌△CDB(SAS),
∴∠ECB=∠DBC,
∴OB=OC,
∴△BOC是等腰三角形.
查看更多完整答案,请扫码查看


